
题目列表(包括答案和解析)
9. 平面上,正三角形ABC與正三角形PQR的面積都為1。三角形PQR的中心M在三角形ABC的邊界上,如果這兩個三角形重疊部份的面積為S,求S的最小值。
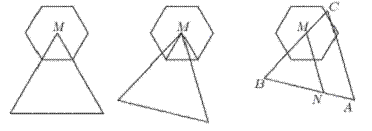
解答:在正△PQR的三個頂點處截去三個全等的正三角形,得到一個面積為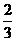 的正六邊形,則M是這個正六邊形的中心。
的正六邊形,則M是這個正六邊形的中心。
若點M與△ABC的一個頂點重合,如左圖,易知正六邊形和△ABC的重疊部分面積是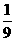 。在中間的圖形中,把△ABC繞著點M順時針旋轉,則始邊所掃過的三角形和終邊所掃過的三角形全等,所以兩個三角形的公共部分面積是不變的。
。在中間的圖形中,把△ABC繞著點M順時針旋轉,則始邊所掃過的三角形和終邊所掃過的三角形全等,所以兩個三角形的公共部分面積是不變的。
若點M在△ABC的邊上,不妨設在BC上,且靠近點C,如右圖所示.,過點M作AC的平行線MN,交邊AB於點N,則△BMN是正三角形.。因為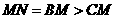 ,BM和MN都與正六邊形相交,所以△BMN與正六邊形的公共部分面積為
,BM和MN都與正六邊形相交,所以△BMN與正六邊形的公共部分面積為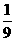 。
。
當把正六邊形恢復成原來的正三角形時,公共部分面積不會減小.,所以兩個三角形公共部分面積的最小值為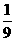 ,如左圖。
,如左圖。
8.
將正整數中所有被4整除以及被4除餘1的數全部刪去,剩下的數依照從小到大的順序排成一個數列
 :2, 3, 6, 7, 10,
11, … 。
:2, 3, 6, 7, 10,
11, … 。
數列 的前n項之和記為
的前n項之和記為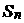 ,其中n=1,
2, 3, …。
,其中n=1,
2, 3, …。
求S=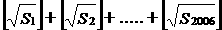 的值。(其中
的值。(其中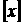 表示不超過x的最大整數)
表示不超過x的最大整數)
解答:易知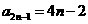 ,
, ,
,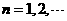 ,因此
,因此
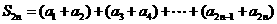
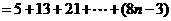
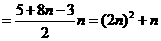 ,
,
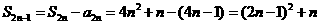 ,
,
所以
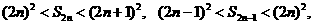
故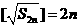 ,
,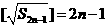 ,從而
,從而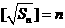 ,於是
,於是

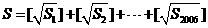
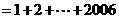
 。
。
7.
設n為任意奇正整數,證明: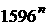 +
+ 能被2006整除。
能被2006整除。
證明:因為 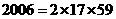 ,所以為證結論成立,只需證
,所以為證結論成立,只需證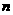 為奇正整數時,
為奇正整數時,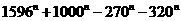 能被2,17,59整除。顯然,運算式能被2整除。
能被2,17,59整除。顯然,運算式能被2整除。
應用公式,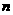 為奇數時,
為奇數時,
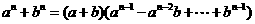 ,
,
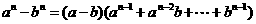 。
。
則由於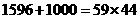 ,
,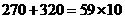 ,所以
,所以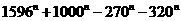 能被59整除。
能被59整除。
又1596-270=1326=17×78,1000-320=680=17×40,所以 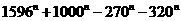 能被17整除。
能被17整除。
故結論成立。
6. 甲和乙在一個n´n的方格表中做填數遊戲,每次允許在一個方格中填入數字0或者1(每個方格中只能填入一個數字),由甲先填,然後輪流填數,直至表格中每個小方格內都填了數。如果每一行中各數之和都是偶數,則規定為乙獲勝,否則當作甲獲勝。請問:
(1) 當n=2006時,誰有必勝的策略?
(2) 對於任意正整數n,回答上述問題。
解答:(1) 當n=2006時,後填數的乙有必勝策略。用1´2的多米諾骨牌對表格進行分割,使得每一行都由1003塊多米諾組成,當甲對某塊多米諾的一個中填數時,乙也在該多米諾中填數,並且使得這塊多米諾中兩個數之和為偶數。依此策略,乙可以使得表格的每一行中各數之和都是偶數。故乙獲勝。
(2) 當n為偶數時,同上述操作,可知乙有必勝策略;當n為奇數時,甲有必勝策略:他可以先在第1行第1列的方格中寫上1,然後對第1行中其餘方格作前面的多米諾分割,採取同樣的操作方式,可使表格中第1行中各數之和為奇數。
5. “幸運數”是指一個等於其各位數碼 (十進位) 和的19倍的正整數,求出所有的幸運數。
解答:設10 a+b是一個至多兩位數,方程 10 a + b = 19 (a + b) 僅當 a = b = 0時成立。所以,所有的幸運數至少是三位數。
假設一個幸運數有m位數,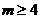 ,則該數至少為
,則該數至少為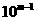 ,其數碼和至多為 9m,所以,
,其數碼和至多為 9m,所以,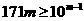 。
。
當 m = 4時,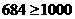 不成立。而
不成立。而 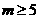 ,更不成立。因此,所有的幸運數都是三位數,由100a + 10b + c = 19a + 19b + 19c,知 9a
= b + 2c。
,更不成立。因此,所有的幸運數都是三位數,由100a + 10b + c = 19a + 19b + 19c,知 9a
= b + 2c。
當 a = 1時,可得 (b,c) = (1,4),(3,3),(5,2),(7,1),(9,0)。
當 a = 2時,可得 (b,c) = (0,9),(2,8),(4,7),(6,6),(8,5)。
當 a = 3時,可得 (b,c) = (9,9)。
當 a > 3時,無解。
所以共有 11 個幸運數: 114, 133, 152, 171, 190, 209, 228, 247, 266, 285 和 399。
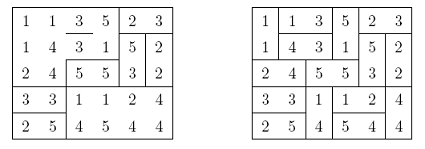
4. 一片骨牌是由兩個單位正方形以邊對邊相連接而成,在每個正方形內標記上數字1、2、3、4或5,所以我們共可得標號為11,12,13,14,15,22,23,24,25,33,34,35,44,45,55的15片不同的骨牌。將這15片骨牌排成一個如圖的5×6的長方形,每片骨牌的邊界已經擦除,請試著把這些骨牌的邊界重新畫出來。

解答:首先,注意到編號為55的骨牌一定是在矩形的中心,而編號22的骨牌只能是在右邊界處。此時,右上角編號為3的骨牌必與右側的2一起組成編號為23的骨牌.。所以,右下角的2只能與5一起組成編號為25的骨牌,而這個2上面的3只能組成33骨牌.。所以,可在圖中,把剩下的33、23對之間用一條線分隔.第三行的3只能與其上的5組成35編號的骨牌.如左圖。
這時,第一行的5不能與其左側的3組成35編號的骨牌,只能與其下的1組成編號為15的骨牌。這使得左側只能為13、34編號的骨牌,這樣,左上角的骨牌為11和24。
在右下角,必須出現編號為12的骨牌,此時,其餘的骨牌也就確定了。
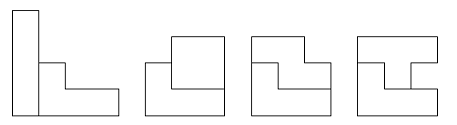
3. 四個單位正方形以邊對邊相連接而成,可以拼成如圖五種不同的形狀。用一片“L”形(圖中第一個)分別與其餘四個中的一片拼成軸對稱圖形,請繪出所有可能之組合。
 解答:
解答:
2. 一個三角形可被剖分成兩個等腰三角形,原三角形的一個內角為36˚,求原三角形最大內角的所有可能值。
解答:(1)若剖分線不過點B。不妨設剖分線為AD,此時△BAD是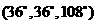 或者
或者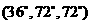 的三角形。
的三角形。
若△BAD是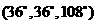 的三角形,則△CAD或者是
的三角形,則△CAD或者是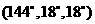 第一個圖,或者是
第一個圖,或者是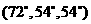 第二個圖,或者
第二個圖,或者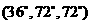 第三、四個圖.
第三、四個圖.

(2) 若剖分線過點B。不妨設為BE,則△CBE必定是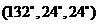 ,△ABE是
,△ABE是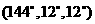 的三角形。
的三角形。
所以原三角形的最大內角可能是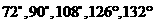 。
。
1. 老師說:「要在一個三邊長為2,2,2x的三角形內部放置一個盡可能大的圓,則正實數x的值該是多少?」
學生A說:「我想x=1。」
學生B說:「我認為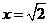 。」
。」
學生C說:「你們回答都不對!」
他們三人誰的回答是正確的?為什麼?
解答:一方面三角形的面積=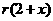 ;另一方面,該三角形底邊上的高為
;另一方面,該三角形底邊上的高為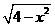 ,所以三角形面積
,所以三角形面積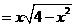 。可得
。可得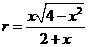 。
。
當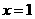 時,
時,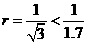 ; 當
; 當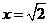 時,
時,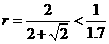 。
。
取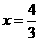 ,則
,則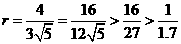 ,所以
,所以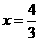 是一個更好的選擇。所以學生C的回答正確。
是一個更好的選擇。所以學生C的回答正確。
註:當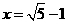 時,可取到r的最大值
時,可取到r的最大值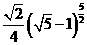 。
。
10. 设m是一个小于2006的四位数,已知存在正整数n,使得m-n为质数,且mn是一个完全平方数,求满足条件的所有四位数m.
解答 由题设条件知:m-n=p,p是质数,则m=n+p,设mn=n(n+p)=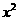 ,其中x是正整数,那么
,其中x是正整数,那么
 ,
,
即
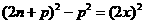 ,
,
于是
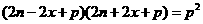 ,
,
注意到p为质数,所以
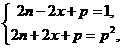
把两式相加得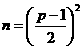 ,进而
,进而 ,结合
,结合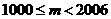 ,可得
,可得 ,于是,质数p只能是67,71,73,79或83.从而,满足条件的m为1156,1296,1369,1600,1764.
,于是,质数p只能是67,71,73,79或83.从而,满足条件的m为1156,1296,1369,1600,1764.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com