1．　 用方程的思想指导解题　　　　　　　　　　　　　 2.　 用整体的思想指导解题

例如：已知求　　　 例如：已知 求

4．用数形结合的方法解三角不等式

例如：已知，求角的取值范围

(1)任意角的三角函数的定义：

　 设是一个任意角，的终边上任意一点P(除端点外)的坐标是(，它与原点的距离是)，那么：比值分别叫的正弦，余弦，正切，余切，正割，余割，记作：sin,

三角函数	定义域	值域
	R	[-1,1]
	R	[-1,1]
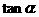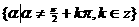		R
	{	R
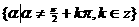		R
	{	R

　(2)正弦线，余弦线，正切线的定义

(3)三角函数符号的判断

口诀记忆法：　 一全正，二正弦，三正切，四余弦

(4)公式一：终边相同的角的同一三角函数值相等

(

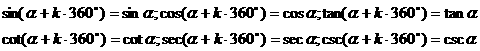(5) 同角三角函数的关系式：

；　 　;　

,　 ,　 　;　

二：任意角的三角函数的方法总结

1：用定义法求三角函数值　　　　　　　　　　　　 2．用转化法求终边相同的交的三角函数值

例题：求的六个三角函数值　　　　　　　　　　　 例如：求值

3．用分类讨论的方法解题

例如：已知角的终边在直线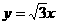上，求角的六种三角函数值

12．(05全国)在△ABC中，已知tan＝sinC，则以下四个命题中正确的是(　)

(1)tanA·cotB＝1．　　　　　　　　　　　　　　　　　　 (2)1＜sinA+sinB≤．

(3)sin²A+cos²B＝1．　　　　　　　　　　　　　　　　　 (4)cos²A+cos²B＝sin²C．

A．①③　　　　　　　　　 B．②④　　　　　　　　　　　 C．①④　　　　　　　　　 D．②③

沙河市一中高一2005－2006学年度下学期

11．已知α.β是锐角，sinα＝x，cosβ＝y，cos(α+β)＝－，则y与x的函数关系式为(　)

A．y＝―+x　 (＜x＜1)　　 B．y＝―+x　 (0＜x＜1)　

C．y＝――x　 (0＜x＜)　　　 D．y＝――x　 (0＜x＜1)

10．在△ABC中，tanA tanB＞1是△ABC为锐角三角形的(　)

　A．充要条件 B．仅充分条件　　 C．仅必要条件　　 D．非充分非必要条件

9．(04江苏)已知0＜α＜，tan+cot＝，则sin(α－)的值为(　)

　A．　　 　B．　 　　　 C． 　　 D．－

8．的值是(　　 )

　　 A．　 　　　　 B．　 　　　　　 C． 　　　　 D．

7．(05春北京)在△ABC中，已知2sinAcosB＝sinC，则△ABC一定是(　　 )

　A．直角三角形　　　　 B．等腰三角形　　　　　　 C．等腰直角三角形 D．正三角形

6．若α满足＝2，则sinα·cosα的值等于(　)

　　 A． 　　　　　 B．－　　 　　　 C．±　 　　　　 D．以上都不对