
题目列表(包括答案和解析)
4.已知点A 若向量
若向量 与
与 同向,
同向, ,则点B的坐标为( )
,则点B的坐标为( )
3.设 是任意的非零平面向量,互相不共线,则下列命题中是真命题的有( )
是任意的非零平面向量,互相不共线,则下列命题中是真命题的有( )
①  ②
② 
③ 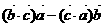 不与
不与 垂直 ④
垂直 ④ 
A ①② B ②③ C ③④ D ②④
2.已知 ,且
,且 ,则
,则 与
与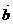 的夹角为 ( )
的夹角为 ( )
A 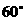 B
B  C
C  D
D 
1.若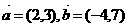 ,则
,则 在
在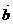 方向的投影为 ( )
方向的投影为 ( )
A  B
B 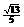 C
C  D
D 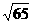
5.
两点间的距离公式:设A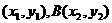 ,则
,则
平移公式描述的是平移前的点与平移后的对应点坐标与平移向量的坐标之间的关系。
平移前的点 平移后的对应点
平移后的对应点
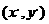 ,平移向量的坐标
,平移向量的坐标
则 
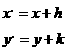
4. 向量数量积的坐标运算。
设 ,则:
,则:
(1) (2)
(2)
(3)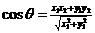 (4)
(4)
3.运算律:(1) (交换律) (2)
(交换律) (2) (与实数的集合律)
(与实数的集合律)
(3) (乘法对加法的分配律)
(乘法对加法的分配律)
没有结合律,可见向量的数量积完全遵循多项式运算法则
2.
数量积的性质:设 是单位向量。<
是单位向量。< (1)
(1)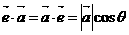
(2)a与b同向时, ;a与b反向的时候
;a与b反向的时候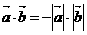 。
。
(3) 或
或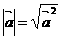 (4)
(4)
 (5)
(5)
1. 数量积的概念
(1) 向量的夹角:如图,已知两个向量a和b,使 =a,
=a, b。则
b。则 叫做响亮a与b的夹角,记为<a,b>
叫做响亮a与b的夹角,记为<a,b>
(2) 数量积的定义:已知两向量a,b的夹角为 ,则数量
,则数量 叫做
叫做
a与b的数量积,记为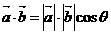
(3)数量积的集合意义:数量积 等于
等于 的模与
的模与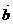 在
在 方向上的投影
方向上的投影
的乘积
4.(本题满分11分,其中第1小题5分,第2小题6分)
设定义域为R的函数 .
.
 (1) 在平面直角坐标系内作出该函数的图像;
(1) 在平面直角坐标系内作出该函数的图像;
(2) 试找出一组 和
和 的值,使得关于
的值,使得关于 的方程
的方程 有7个不同的实根.请说明你的理由.
有7个不同的实根.请说明你的理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com