
题目列表(包括答案和解析)
4. 作业:
1).已知
2).已知 的两根,则
的两根,则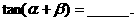
3).已知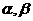 为锐角,且
为锐角,且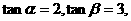 ,则
,则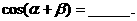
4).已知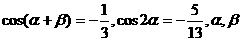 均为锐角,求
均为锐角,求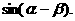
5).已知 且求
且求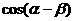 的值. <
的值. <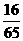 >
>
6). 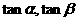 是二次方程
是二次方程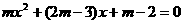 的两根,求函数
的两根,求函数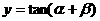 的最小值. <
的最小值. <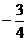 >
>
3. 典型例题分析:
<1>.求值问题:
(1)给角求值:
例1:求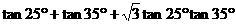 的值. <
的值. <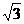 >
>
析:观察非特殊角与特殊角之间的关系,将非特殊角转化为特殊角求解,由公式
Ex: ①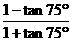
②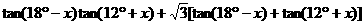
(2)给值求值:
例2.已知
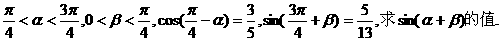 析: 若将
析: 若将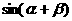 按和角公式展开,通过求
按和角公式展开,通过求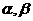 的正,余弦求值较复杂,若观察到
的正,余弦求值较复杂,若观察到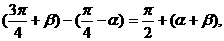 便可用整体思想求解,较简捷.
便可用整体思想求解,较简捷.
Ex: 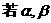
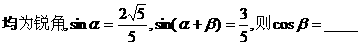 <B>
<B>
A.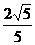 B.
B. C.
C.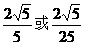 D.
D.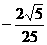
① 给角求值:
例3: 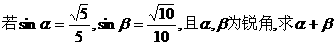 的值. <
的值. <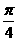 >
>
析: 注意未知角与已知角的联系,其关键在于对角的范围的讨论,注意根据某些条件缩小角的范围,求出准确角.
Ex: 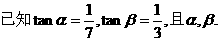 均为锐角,求
均为锐角,求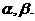 <
<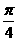 >
>
② 给式求值:
例4:  <
<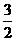 >
>
析: 可将已知式或所求式进行化简,再求值,常用方法有:①消去法;②解方程;③应用比例性质.
Ex: 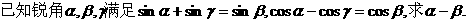 <-
<-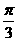 >
>
<2>.化简问题:
例5:化简①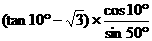 ;
;
② .
.
析: 涉及弦,切的问题,需将”切化弦”,再利用和(差)角公式化简.
Ex: 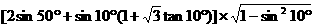
<3>.证明问题:
例6: 已知
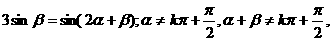

析: 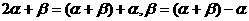
Ex: 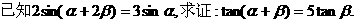
总结: 利用和(差)角三角函数公式进行化简,求值,证明问题时,要注意公式成立的条件,熟练地掌握公式的顺用,逆用,变形用,并注意各种解题技巧.
2. 方法罗列:
① 直接应用和(差)角公式进行求值,化简,证明.
② “整体换元”,注意找未知量与已知量间的联系,并注意其公式成立的条件.
1. 考点梳理: 两角和与差的三角函数公式:
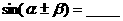
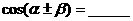
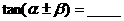
<注: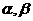 指任意角,熟记和(差)角公式特点>
指任意角,熟记和(差)角公式特点>
正.余弦及正切的和(差)角公式的”正用” ,”逆用”,变形使用”
16.若lgx , lg(x-2y) , lgy成等差数列,则log
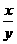 =
=
洛阳市名校联考:2004-2005学年上学期月考试卷
15.若 A是B的充分不必要条件,则A是
A是B的充分不必要条件,则A是 B的
B的
14.函数y=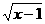 +1(x≥1)的反函数为
+1(x≥1)的反函数为
13.函数y=log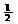 (x2-x)的递增区间为
(x2-x)的递增区间为
12.函数y=logax在[2,+ ∞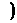 上恒有|y|>1,则实数a的取值范围是
上恒有|y|>1,则实数a的取值范围是
A. (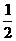 ,1)∪(1,2) B.
(0,
,1)∪(1,2) B.
(0,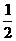 )∪(1,2)
)∪(1,2)
C. (1,2)
D.
(0,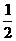 )∪(2,+ ∞)
)∪(2,+ ∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com