
题目列表(包括答案和解析)
4、 O是平面内一定点,A,B,C是平面内不共线的三个点,动点P满足 =
= +λ(
+λ( +
+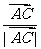 ),λ≥0,则P的轨迹一定通过△ABC的 ( )
),λ≥0,则P的轨迹一定通过△ABC的 ( )
A、外心 B、内心 C、重心 D、垂心
3、 已知任意四边形ABCD的边AD,BC的中点分别为E,F,等式2
 =
= +
+ 成立吗?试给出证明.
成立吗?试给出证明.
2、 已知A(1,3),B(-1,-1),C(3,3),D(4,1),求一点E,使得A,B,E三点共线,C,D,E三点也共线.
例1、 已知A(-1,2),B(2,8)及 =
=
 ,
, =
=
 ,求C,D的坐标。
,求C,D的坐标。
例2、 设平行四边形ABCD中, =4
=4 ,
, =5
=5 。求证E,F,C三点共线。
。求证E,F,C三点共线。


 A
D
A
D
E
B C
变式1、5 =4
=4 +5
+5 ,5
,5 =
= +5k
+5k ,若E,F,C三点共线,求k的植。
,若E,F,C三点共线,求k的植。
变式2、5 =4
=4 +
+ ,
, =4
=4 ,若E,F,C三点共线,求
,若E,F,C三点共线,求
例3、设四边形ABCDDE的对角线AC,BD的中点分别是E,F,设 =
=  ,
, =
=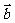 .
.
1) 试用 ,
, 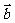 表示
表示
 。2)求证
。2)求证 | CD-AB|≤ EF≤
| CD-AB|≤ EF≤ (CD+AB)
(CD+AB)
例4、已知G为△ABC的重心,P为平面上任一点,求证:
作业:
1、 在平行四边形ABCD中,点M是AB的中点,点N在BD上,3BN=BD,求证M,N,C三点共线.






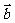


 +
+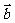


 +
+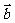
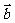
三角形法则 平行四边形法则
(1)

 运算性质:
运算性质:
 +
+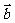 =
=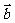 +
+  (交换律) (
(交换律) ( +
+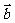 )+
)+ =
= +(
+(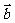 +
+ ) (结合律)
) (结合律)  +0=0+
+0=0+  =
= 
(2)
 减法运算
减法运算
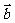

 -
-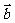 三角形法则
三角形法则
(4) 实数与向量的积 定义: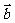 =λ
=λ ,其中λ>0时,λ
,其中λ>0时,λ 与
与 同向,|λ
同向,|λ |=|λ| |
|=|λ| |  |
|
当λ<0时,λ 与
与 反向,|λ
反向,|λ |=|λ| |
|=|λ| |  |=-(-λ)|
|=-(-λ)|  |, 特殊地0
|, 特殊地0  =0
=0
(5)
共线定理:向量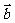 与非零向量
与非零向量 共线的充要条件是有且只有一个实数λ,使
共线的充要条件是有且只有一个实数λ,使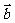 =λ
=λ .
.
平面向量基本定理:如果 ,
,  是同一平面内的两个不共线向量。那么对于这一平面内的任一向量
是同一平面内的两个不共线向量。那么对于这一平面内的任一向量 ,有且只有一对实数λ1,λ2,使
,有且只有一对实数λ1,λ2,使 =λ1
=λ1 +λ2
+λ2 , 把不共线的向量
, 把不共线的向量 ,
, 叫做表示这一平面内所有向量的一组基底。
叫做表示这一平面内所有向量的一组基底。
22.在倾角为30°的斜面上有一块坚直放置的挡板,在挡板和斜面之间有一个重为20N的光滑圆球,求这个球对斜面的压力和对挡板的压力。(14分)
21.已知O为△ABC的外心,H为垂心,求证: 。(14分)
。(14分)
20.飞机从A地按北偏西75°的飞向飞行400km后到达B地,然后向C地飞行。已知C地从A地西偏南30°的方向处,且A,C两地相距为 ,求飞机从B地向C地飞行的方向,及B,C两地的距离。(12分)
,求飞机从B地向C地飞行的方向,及B,C两地的距离。(12分)
19.一艘船以7km/h的速度向垂直于对岸的方向行驶,同时河水的流速为3km/h。求航船实际航行速度大小和方向。(12分)
18.飞机按东偏北25°从甲地飞行300km到达乙地,再从乙地按北偏西25°飞行400km到达丙地,求甲丙两地之间的距离。(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com