
题目列表(包括答案和解析)
9、取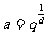 即可,其中
即可,其中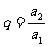 ,
,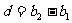
8、证:∵2b=a+c,x2=ab,y2=bc. ∴x2+y2=(a+c)b=2b2,故x2、b2、y2成等差数列。
7、略
6、(1) 略 (2) an = 6n -3
5、证明:∵ ,∴
,∴
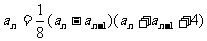 ,即
,即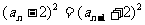
而 ,∴
,∴ .
.
即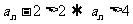 ,∴
,∴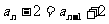 ,∴
,∴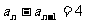 .
.
∴ 是等差数列,或
是等差数列,或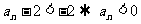 (舍去),
(舍去), =2.
=2.
4、略
2、首项a1=2,公比q=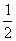
2、当n≥2时,由题设,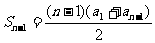 ,
,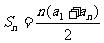 .
.
所以
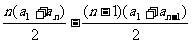 .
.
同理有
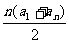
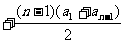 .
.
整理得an+1-an=an-an-1,对于任意n≥2成立,
因此an+1-an=an-an-1=…=a2-a1,从而{an}是等差数列。
1、q + q2 + q3 是等比数列第2 , 3 , 4 项之和与第一项的比值.
10、设An为数列 前n 项的和,An
=
前n 项的和,An
=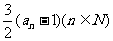 。数列
。数列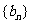 的通项公式为
的通项公式为
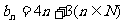 .若
.若 ,则称
,则称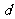 为数列
为数列 与
与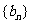 的公共项。将数列
的公共项。将数列 与
与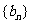 的公共项,按它们在原数列中的先后顺序排成一个新的数列
的公共项,按它们在原数列中的先后顺序排成一个新的数列 ,证明数列
,证明数列 的通项公式为
的通项公式为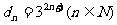 .
.
答案提示
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com