5、证明： (1)a₁=S₁=, a_n=S_n－S_n–1=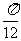(4n－1) (n≥2),且当n=1时,a₁==S₁,

∴a_n=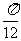(4n－1) (nN). 　∵a_n+1－a_n=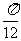[4(n－1)－1]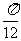－(4n－1)=,

∴{a_n}是以为首项,为公差的等差数列.

4、解： (1)∵n=1时,a₁=S₁=9,n≥2时,a_n=S_n－S_n–1=(10ⁿ－1)－(10^n–1－1)=9·10^n-1,且当n=1时, 有a₁=S₁=9;∴a_n=9·10^n–1(n≥1).

(2) ∵n=1时,a₁=3¹+1=4, n≥2时,a_n=S_n－S_n–1=(3ⁿ+1)－(3^n–1+1)=2·3^n–1,且当n=1时,a₁=2·3⁰=2S₁=4,∴a_n=.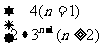

3、求得d=0.4,a₁=-1.3，原式＝(a₁₈+a₂₂)+(a₁₉+a₂₁)+a₂₀=5(a₁+19d)=31.5.

1、0，4，8，16或15，9，3，1　2、(1)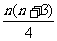；(2)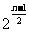

15、将自然数按下表排列：

　　 1　 2　 5　 　10　 17　 …

　　 4　 3　 6 　11　 18　 …

　　 9　 8　 7 　12　 19　 …

　　 16　 15　 14　 13　 20　 …　

　　 25　 24　 23　 22　 21　 …　

　　 ……

(1)第1列中第m个数是多少？ 第1行中第n个数是多少？(2)若m≥n，则第m行(自上而下)、第n列(自左而右)的数是多少？若m＜n呢？(3)99在上起第几行、左起第几列？翰林汇

答案提示

14、数列前n项之和Sn=3ⁿ+a(a为常数)，a取何值时此数列成等比数列？

13、在等比数列{a_n}中，已知前10项和为5，前20项和为15，求前30项和。

12、数列{a_n}既是等差数列又是等比数列。①求证该数列必是常数列；②若a_n+1=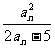，求该数列前200项的和。

11、某鱼塘养鱼,由于改进了饲养技术,预计第一年的增长率为200%,以后每年的增长率是前一年的一半,设原来的产量为a，由于存在池塘老化及环境污染等因素，估计每年将损失年产量的10%，照这样下去，以后每年的产量是否始终是逐年提高的？若是，请给予证明；若不是，请说明从第几年起，产量将不如上一年(参考数据lg2=0.3010,lg3=0.4771)

10、等差数列{a_n}中, 其前10项和为100, 而前100项的和为10, 求前110项和.