
题目列表(包括答案和解析)
1.设等差数列{an}的前n项和Sn=12n-n2,
(1)求a10+a11+a12+…+a20的值;并证:{an}为等差数列.
(2)求Sn的最值. (3) 求数列{|an|}}的前n项和.

4.设数列{an}的前n项和为Sn=a1+a2+…+an,则an=____________________________
[知识点训练]

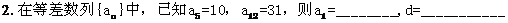

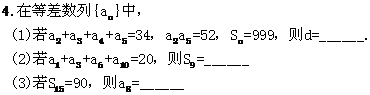
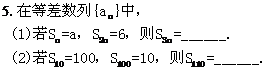
[典型例题]
2.等差数列的前n项和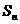 :(1)___________________ (2)_______________________
:(1)___________________ (2)_______________________

1.等差数列的通项公式:⑴_______________________ (2)________________________
2.理解等差数列概念及推导通项公式的方法;掌握求和公式并能加以灵活应用.
[双基回顾]
19.十七世纪意大利的赌徒们认为:两颗骰子掷出的点数和为5和与掷出的点数和为9的概率是相等的,你认为他们的看法对吗?为什么?
解:抛两颗骰子的结果总数为6×6=36
设A=“点数之和为5”,则A包含的基本事件的个数为4个,其概率为P(A)=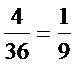
设B=“点数之和为9”,则事件B包含的基本事件的个数为4个,其概率为P(B)=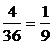
所以 P(A)=P(B) 即他们的说法是正确的。
18.平面上画了一些彼此相距2a 的平行线,把一枚半径r<a的硬币任意掷在平面上,求硬币不与任一条平行线相碰的概率


解:设事件A:“硬币不与任一条平行线相碰”,为了确定硬币的位置,由硬币中心O向靠得最近的平行线引垂线OM,垂足为M,如上图所示,这样线段OM的长度(记作│OM│)的取值范围是[0,a] ,其长度就是几何概型定义中区域Ω的几何度量,只有当r<│OM│≤a时硬币不与平行线相碰,其长度就是子区域A的几何度量,所以
P(A)=
16.在一次口试中,要从5道题中随机抽出3道题进行回答,答对其中的2道题就获得优秀,答对其中的1道就获得及格,某考生会回答5道题中的2道题,试求:
(1) 他获得优秀的概率是多少?
(2) 他获得及格与及格以上的概率是多大?
解:从5道题中任取3道回答,共有(1,2,3),(1,2,4),(1,2,5)
(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,4,5),(3,4,5)
10个基本事件。
(1)设A={ 获得优秀},则随机事件A包含 基本事件个数m=3种
;故事件A的概率为P(A)=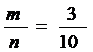
(2)设B={获得及格与及格以上},则事件B所包含的基本事件个数
m=9种,故事件B的概率P(B)=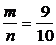
答:这个考生获得优秀的概率为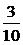 ,获得及格与及格以上的概率为
,获得及格与及格以上的概率为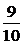 。17.从1,2,3,4,5五个数字中,任意有放回地连续抽取三个数字,求下列事件的概率:
。17.从1,2,3,4,5五个数字中,任意有放回地连续抽取三个数字,求下列事件的概率:
(1)三个数字完全不同;
(2)三个数字中不含1和5 ;
(3)三个数字中5恰好出现两次
解:从五个数字中,任意有放回地连续抽取三个数字,相当于完成这件事分三步,每步从5个元素中均取出一个元素,有5种不同的方法,因此共有5×5×5=125种不同的结果。
(1)三个数字完全不同相当于第一步有5种方法,第二步有4种方法,第三步有3种方法,故有5×4×3=60种,所以三个数字完全不同的概率为
P1=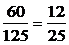 .
.
(2) 三个数字中不含1和5,相当于每次只能从其他三个数字中有放回地抽取出一个数字,故共有33=27种,因此概率P2=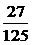
(3)先研究第一次5,第二次5,第三次非5的方法数,相当于第一次取5,第二次取5,第三次取非5,共有1×1×4=4种不同的方法,所以恰有两次取5的方法数为12种,所以三个数字种5恰好出现两次的概率为P3=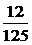
15.某人进行射击表演,已知击中10环的概率为0.35,击中9环的概率为0.30,击中8环的概率为0.25,现在他射击一次,问击中8环以下(不含8环)的概率是多少?
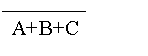 解:记=“击中10环” ,B=“击中9环” ,C=“击中8环” ,D=“击中8环以下”
则:D=
,且A、B、C互斥,
解:记=“击中10环” ,B=“击中9环” ,C=“击中8环” ,D=“击中8环以下”
则:D=
,且A、B、C互斥,
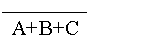 所以 P(D) =P(
)
所以 P(D) =P(
)
=1-P(A+B+C) =1-[P(A)+P(B)+P(C)]
= 1-[0.35+0.30+0.25]=0.1
10. 在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于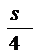 的概率是(C
)
的概率是(C
)
 A.
A.
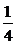 B
B 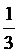 C
C 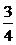 D
D 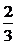
二 填空题 (每题5分 共 5分×4=20分 )
11 抛掷一个骰子的一次试验,事件A表示奇数点向上,事件B表示向上的点数不超过3,则P(A+B)= 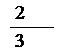
12 袋中有5个白球,3个黑球,从中任取3个球,则至少有一个白球的概率是 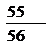
13 从甲、乙、丙、丁四人中选两名代表,甲被选中的概率是 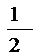
14 在区间(0,L)内任取两点,则两点间的距离小于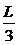 的概率
的概率 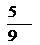
三 解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com