
题目列表(包括答案和解析)
6、设α,β是一个钝角三角形的两个锐角,下列四个不等式中不正确的是 ( )
A.tanαtanβ<1
B.sinα+sinβ<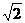
C.cosα+cosβ>1
D.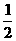 tan(α+β)<tan
tan(α+β)<tan
5、已知关于x的方程2cosx+6sinx+1=0的两根分别为α、β,且α、β∈(0,2π),α≠β,则
sin(α+β)等于 ( )
A.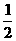 B.
B.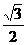
C.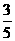 D.
D.
4、已知tan(α+β) =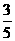 , tan(β-
, tan(β- )=
)=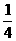 ,那么tan(α+
,那么tan(α+ )为 ( )
)为 ( )
A.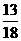 B.
B. C.
C.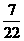 D.
D.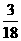
3、设t = sinθ+cosθ,且sin3θ+cos3θ<0,则t的取值范围是 ( )
A.[-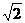 ,0] B.(-1,0)∪(1,
,0] B.(-1,0)∪(1, 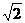 )
)
C.[-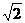 ,
, 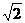 ]
D.(-
]
D.(- ,0)∪(
,0)∪( ,+ ∞)
,+ ∞)
2、函数f(x) =  的值域为 ( )
的值域为 ( )
A. B.
B.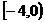 C.[-4,0] D.[0,4]
C.[-4,0] D.[0,4]
1、函数y=sinxcosx+ cos2x-
cos2x-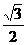 的最小正周期是 ( )
的最小正周期是 ( )
A.π B.2π C. D.
D.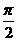
17 (本小题满分12分)
已知等比数列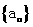 中,
中,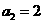 ,
,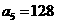 .
.
(I) 求通项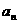 ;
;
(II) 若 ,
, 数列的前
数列的前 项和为
项和为 ,且
,且 ,求
,求 的值.
的值.
18 (本小题满分12分)
从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为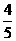 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为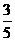 .试求:
.试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率;
(II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率.
19 (本小题满分12分)
已知向量 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量 =(2,0)的夹角为
=(2,0)的夹角为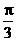 ,其中A, B, C是
,其中A, B, C是 ABC的内角.
ABC的内角.
(I)求角B的大小; (II)求sinA+sinC的取值范围.
20 (本小题满分12分)
已知函数 ,若函数
,若函数 图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
图象上任意一点P关于原点的对称点Q的轨迹恰好是函数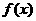 的图象.
的图象.
(1)写出函数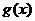 的解析式;
的解析式;
(2)当 时,总有
时,总有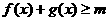 成立,求实数
成立,求实数 的取值范围.
的取值范围.
21 (本小题满分12分)
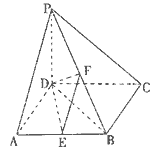
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点.
(1)求证:EF⊥CD;
(2)求DB与平面DEF所成角的大小;
(3)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.
22 (本小题满分14分)
设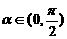 ,函数
,函数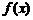 的定义域为
的定义域为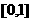 ,且
,且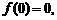
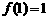 ,对定义域内任意的
,对定义域内任意的 ,满足
,满足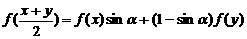 ,
,
求:(1) 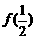 及
及 的值; (2)函数
的值; (2)函数 的单调递增区间;
的单调递增区间;
(3) 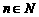 时,
时,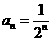 ,求
,求 ,并猜测
,并猜测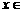
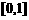 时,
时,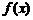 的表达式.
的表达式.
06届南通市小海中学期中考试试卷 2005-11
13已知 |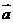 |=1,|
|=1,|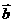 |=
|= ,若
,若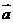 //
//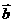 且
且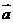 与
与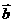 同向,则
同向,则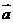 ·
·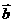 ____________.
____________.
14已知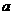 为实数,
为实数,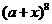 展开式中
展开式中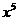 的系数为
的系数为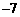 ,则
,则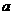 =____________.
=____________.
15 在 中,
中,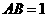
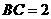 ,
, ,则
,则 _______.
_______.
16在数列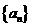 中,
中, ,
, ,则数列{an}的通项公式
,则数列{an}的通项公式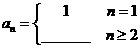
06届南通市小海中学期中考试试卷 2005-11
数学试卷
第Ⅱ卷(非选择题,共90分)
1设全集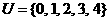 ,集合
,集合 ,
,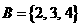 ,则
,则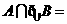 ( )
( )
A  B
B 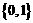 C
C  D
D 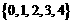
2已知数列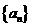 的前
的前 项和为
项和为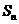 ,且
,且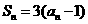 则
则 等于 ( )
等于 ( )
A 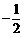 B
B  C
C  D
D 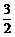
3不等式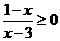 的解集是 ( )
的解集是 ( )
A  B
B 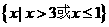 C
C 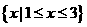 D
D 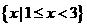
4给定两个向量 ,
, ,若
,若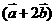 与
与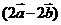 平行,则x的值等于( )
平行,则x的值等于( )
A 1 B 2 C  D
D 
5对于数列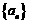 ,“对任意
,“对任意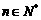 ,点
,点 都在直线
都在直线 上”是“
上”是“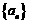 为等差数列”的
( )
为等差数列”的
( )
A 充分不必要条件 B 必要不充分条件
C 充要条件 D 既不充分也不必要条件
6已知抛物线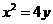 ,则它的焦点坐标是
( )
,则它的焦点坐标是
( )
A  B
B 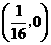 C
C 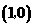 D
D

7若y = x + b与y = ax + 3互为反函数,则 a + b = ( ) A -2 B 2 C 4 D -10
8若要得到函数y=sin(2x- )的图像,可以把函数y=sin2x的图像
( )
)的图像,可以把函数y=sin2x的图像
( )
A 向右平移 个单位
B 向左平移
个单位
B 向左平移 个单位
个单位
C 向左平移 个单位
D 向右平移
个单位
D 向右平移 个单位
个单位
9函数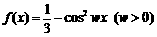 的周期与函数
的周期与函数 的周期相等,则
的周期相等,则 等于 ( )
等于 ( )
A 2 B 1 C  D
D 
10函数f(q ) = 的最大值和最小值分别是 ( ) A 最大值 和最小值0 B 最大值不存在和最小值
C 最大值 -和最小值0 D 最大值不存在和最小值-
11函数 在x=
在x= 处有极值,则
处有极值,则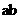 的值为
( )
的值为
( )
A 3 B -3 C 0 D 1
12已知数列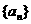 前n项和为
前n项和为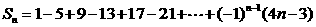 ,
,
则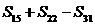 的值是
( )
的值是
( )
A 13 B -76 C 46 D 76
选择题答案填在下面表格内:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com