
题目列表(包括答案和解析)
1、用不等式表示不等关系
例1、某电脑用户计划用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装软件,根据需要,软件至少买3片,磁盘至少买2盒,写出满足上述不等关系的不等式。
例2、咖啡馆配制两种饮料,甲种饮料用奶粉、咖啡、糖,分别为9g、4g、3g;乙种饮料用奶粉、咖啡、糖,分别为4g、5g、5g.已知买天使用原料为奶粉3600g,咖啡2000g,糖3000g。写出配制两种饮料杯数说所满足的所有不等关系的不等式。
2、基本不等式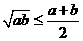 几何意义是“半径不小于半弦”
几何意义是“半径不小于半弦”
3.典型例题
1、如果a,b是正数,那么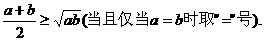
4、求线性目标函数在线性约束条件下的最优解的步骤:
(1)寻找线性约束条件,线性目标函数;
(2)由二元一次不等式表示的平面区域做出可行域;
(3)在可行域内求目标函数的最优解
3、线性规划的有关概念:
①线性约束条件:在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.
③线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
④可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
2、二元一次不等式表示哪个平面区域的判断方法
由于对在直线Ax+By+C=0同一侧的所有点(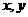 ),把它的坐标(
),把它的坐标(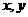 )代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)
)代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)
1、用二元一次不等式(组)表示平面区域
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)
一元二次不等式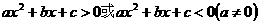 的解集:
的解集:
设相应的一元二次方程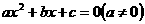 的两根为
的两根为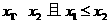 ,
,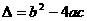 ,则不等式的解的各种情况如下表:(课本第86页的表格)
,则不等式的解的各种情况如下表:(课本第86页的表格)
|
|
 |
 |
 |
|
二次函数  ( 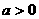 )的图象 )的图象 |
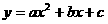 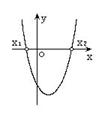 |
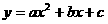 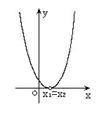 |
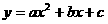 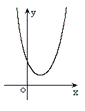 |
一元二次方程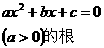 |
有两相异实根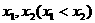 |
有两相等实根 |
无实根 |
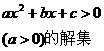 |
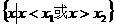 |
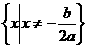 |
R |
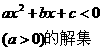 |
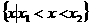 |
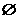 |
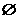 |
2、应用不等式的性质比较两个实数的大小; 作差法 3、应用不等式性质证明
1、应用不等式(组)表示不等关系;
不等式的主要性质:
(1)对称性: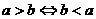 (2)传递性:
(2)传递性: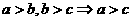
(3)加法法则: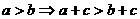 ;
;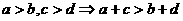
(4)乘法法则: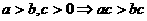 ;
;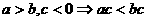
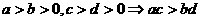
(5)倒数法则: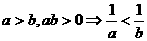
(6)乘方法则: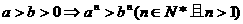
(7)开方法则: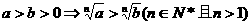
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com