
题目列表(包括答案和解析)
3.如果两条直线a 和b没有公共点,那么a与b的位置关系是 ( )
(A)共面 (B)平行 (C)异面 (D)平行或异面
2.若OA//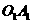 ,OB//
,OB//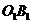 ,则下列结论正确的是
( )
,则下列结论正确的是
( )
(A) =
=  (B)
(B) +
+ =
=
(C) =
= 或
或 +
+ =
= (D)以上都不对
(D)以上都不对
1.下列叙述中,正确的是 ( )
(A)因为P
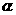 ,Q
,Q
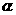 ,所以PQ
,所以PQ
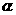 (B)因为P
(B)因为P
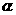 ,Q
,Q
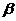 ,所以
,所以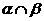 =PQ(C)因为AB
=PQ(C)因为AB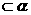 ,C
,C AB,D
AB,D AB,所以CD
AB,所以CD
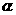
(D)因为AB ,AB
,AB
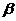 ,所以A
,所以A (
(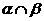 )且B
)且B (
(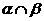 )
)
22.解:(1) a·b=cos2xcos x+sin2xsin x=cos x 2分
(2) ∵| a+b |2=| a | 2+2 a·b+| b |2=2+2cos x= ,∴| a+b | =2| cos
,∴| a+b | =2| cos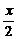 |
同理:| a-b|=2| sin
|
同理:| a-b|=2| sin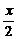 | 4分
∴当m=3时,f (x)=3| a+b |+3| a-b |=6| cos
| 4分
∴当m=3时,f (x)=3| a+b |+3| a-b |=6| cos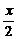 |+6| sin
|+6| sin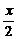 |
∴
|
∴ 即有
即有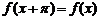 6分
6分
(3) 当m≠3时,f (x)=3| a+b|+m | a-b |=6| cos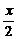 |+2m| sin
|+2m| sin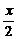 |
∵
|
∵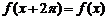 ,∴f (x) 的周期是
,∴f (x) 的周期是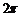 ,故可设0≤x≤
,故可设0≤x≤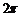 8分
①当0≤x≤
8分
①当0≤x≤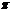 时,0≤
时,0≤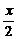 ≤
≤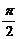 ,
∴
,
∴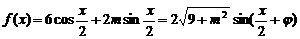 其中
其中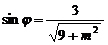 ,
,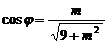 ,且j Î(0,
,且j Î(0,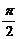 ) 10分
∵
) 10分
∵
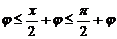 ,∴f (x)的最小值为:
,∴f (x)的最小值为:
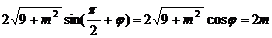 由2m = 1得
由2m = 1得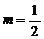 12分
② 当p≤x≤2p 时,
12分
② 当p≤x≤2p 时,
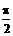 £
£ 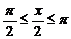 ∴
∴ 其中
其中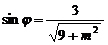 ,
,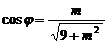 ,且j Î(0,
,且j Î(0,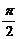 )
∵
)
∵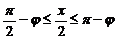 ,同理可得:
,同理可得: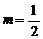 综上,存在
综上,存在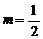 ,使f (x
)的最小值为1.
,使f (x
)的最小值为1.
21.解:由f (x)是偶函数,得f (-x)=f (-x)
即: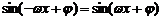 ,所以-
,所以-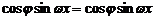 对任意x都成立,且
对任意x都成立,且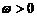 ,∴
,∴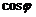 =0
依题设0≤
=0
依题设0≤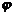 ≤
≤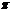 ,故解得
,故解得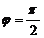 4分
由f(x)的图象关于点M对称,得
4分
由f(x)的图象关于点M对称,得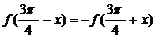 取x=0,得
取x=0,得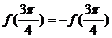 ,所以
,所以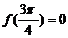 ∵
∵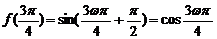 ,∴
,∴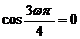 ∴
∴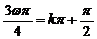 Þ
Þ  ,k=0,1,2,…… 8分
当k=0时,
,k=0,1,2,…… 8分
当k=0时,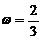 ,
,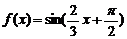 在[0,
在[0,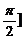 上是减函数
当k=1时,
上是减函数
当k=1时,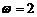 ,
,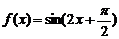 在[0,
在[0,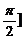 上是减函数
当k≥2时,
上是减函数
当k≥2时,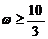 ,
, 在[0,
在[0,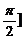 上不是单调函数
∴
上不是单调函数
∴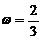 或
或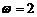 . 12分
. 12分
20.(1)解:由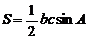 及
及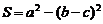 得:
得:
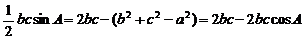 2分
∴
2分
∴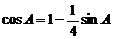 Þ
Þ  Þ
Þ 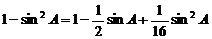 ,即17sin2A-8sinA=0 4分
又sinA≠0,∴
,即17sin2A-8sinA=0 4分
又sinA≠0,∴ 6分
6分
(2)解:∵ ,∴由正弦定理得b+c=16 8分
由(1)得
,∴由正弦定理得b+c=16 8分
由(1)得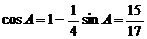 ,
,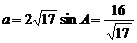 由余弦定理得
由余弦定理得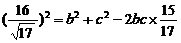 即
即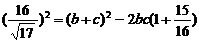 ,解得bc=64 10分
∴
,解得bc=64 10分
∴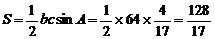 12分
12分
19.(1)解:由图象知,函数的周期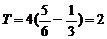 ,∴
,∴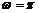 2分
又函数的最大值为2,最小值为-2,∴
2分
又函数的最大值为2,最小值为-2,∴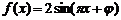 4分
∵当
4分
∵当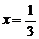 时,函数取最大值,∴可取
时,函数取最大值,∴可取 ,
, 故
故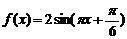 6分
6分
(2解:当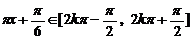 ,即
,即 时,函数是增函数
∴函数的单调递增区间是
时,函数是增函数
∴函数的单调递增区间是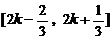 (k∈Z)
当
(k∈Z)
当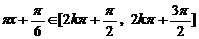 ,即
,即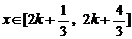 时,函数是减函数
∴函数的单调递减区间是
时,函数是减函数
∴函数的单调递减区间是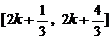 (k∈Z) 8分
(3)解:①把函数y=sin x的图象上各点的横坐标不变,纵坐标伸长到原来的2倍,得到函数y=2sin x的图象;
②把函数y=2sin x的图象向左平移
(k∈Z) 8分
(3)解:①把函数y=sin x的图象上各点的横坐标不变,纵坐标伸长到原来的2倍,得到函数y=2sin x的图象;
②把函数y=2sin x的图象向左平移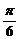 个单位,得到函数
个单位,得到函数 的图象;
③把函数
的图象;
③把函数 的图象上的各点的纵坐标保持不变,横坐标压缩为原来的
的图象上的各点的纵坐标保持不变,横坐标压缩为原来的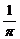 ,得到函数
,得到函数 的图象. 12分
的图象. 12分
18.解:∵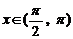 ,∴cos x≠0
在
,∴cos x≠0
在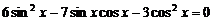 两边同除以cos2x得:
两边同除以cos2x得:
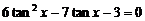 , 2分
解得
, 2分
解得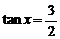 或
或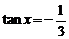 ∵
∵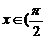 ,
,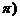 ,∴
,∴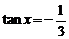 4分
故
4分
故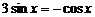 又
又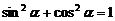 ,∴
,∴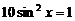 ,因此
,因此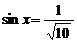 ,
,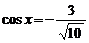 6分
故
6分
故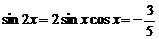 ,
,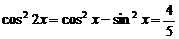 故
故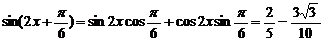 12分
12分
17.(1)证明:∵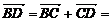 (2e1+8e2)+(3e1-3e2)=5 e1+5e2=5
(2e1+8e2)+(3e1-3e2)=5 e1+5e2=5 2分
∴
2分
∴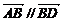 ,又
,又 与
与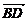 有共同点B 4分
∴ A、B、D三点共线 6分
有共同点B 4分
∴ A、B、D三点共线 6分
(2) 解:∵me1+e2与e1-e2垂直
∴(m e1+e2)·(e1-e2)=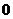 ,即me
,即me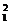 +(1-m)e1·e2-e
+(1-m)e1·e2-e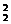 =0 8分
∵|e1|=2,|e2|=3,e1与e2的夹角为60°
∴e
=0 8分
∵|e1|=2,|e2|=3,e1与e2的夹角为60°
∴e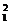 =| e1|2=4,e
=| e1|2=4,e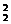 =| e2|2=9,e1·e2=| e1|·| e2|cos
=| e2|2=9,e1·e2=| e1|·| e2|cos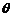 =2×3×cos60°=3 10分
∴4m+3(1-3m)-9=0,m=6. 12分
=2×3×cos60°=3 10分
∴4m+3(1-3m)-9=0,m=6. 12分
17.(12分)设两个非零向量e1和e2不共线.
(1)如果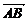 =e1+e2,
=e1+e2, =2e1+8e2,
=2e1+8e2, =3e1-3e2,求证:A、B、D三点共线;(2)若| e1 |=2,| e2
|=3,e1与e2的夹角为60°,me1+e2与e1-e2垂直,求实数m的值.
=3e1-3e2,求证:A、B、D三点共线;(2)若| e1 |=2,| e2
|=3,e1与e2的夹角为60°,me1+e2与e1-e2垂直,求实数m的值.
18(12分)已知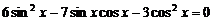 ,
,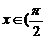 ,
,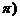 ,求
,求 的值.
的值.
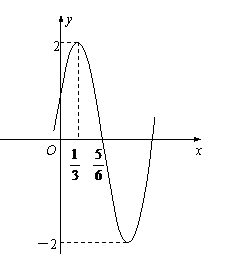 19(12分)已知函数
19(12分)已知函数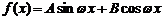 (其中A、B、
(其中A、B、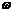 是常数,且A>0,
是常数,且A>0,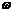 >0)的部分图象如图. (1)求函数f (x)的表达式; (2)写出函数f (x)的单调区间;
(3)指出函数f (x)的图象可以由正弦函数y=sin x的图象如何变换得到.
>0)的部分图象如图. (1)求函数f (x)的表达式; (2)写出函数f (x)的单调区间;
(3)指出函数f (x)的图象可以由正弦函数y=sin x的图象如何变换得到.
20(12分)已知△ABC的面积为S,外接圆半径R=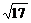 ,a、b、c分别是角A、B、C的对边,设
,a、b、c分别是角A、B、C的对边,设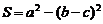 ,
, ,求sin A的值和△ABC的面积.(正弦定理:
,求sin A的值和△ABC的面积.(正弦定理: )
)
21(12分)已知函数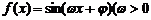 ,0≤φ≤π)是R上的偶函数,其图象关于点M(
,0≤φ≤π)是R上的偶函数,其图象关于点M(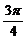 ,0)对称,且在区间[0,
,0)对称,且在区间[0,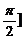 上是单调函数,求φ和
上是单调函数,求φ和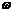 的值.
的值.
22(14分)已知向量a=(cos2x,sin2x),b=(cos x,sin x) (x ÎR), 设f (x)=3 | a+b |+m | a-b | (m为正常数).(1)求a·b;(2)当m=3时,求证:f (x+p )=f (x )对一切实数x恒成立;(3)当m≠3时,函数f (x)的最小值是否能等于1,若能,请求出m的值,若不能,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com