
题目列表(包括答案和解析)
1.设全集I={a,b,c,d},集合M={a,b,c},集合N={b,d},P={a,c,d},则( )
A. P=(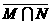 ) B. P=(M∪N)
C. N=(M∩P) D. N=
) B. P=(M∪N)
C. N=(M∩P) D. N=
∴不等式的解集为{X|-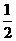 t2-2≤X≤
t2-2≤X≤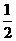 t2+1}.
t2+1}.
(2)对于含有几个绝对值的代数式或不等式,可以用零点分段的方法去掉绝对值符号. 例7 (1)解方程:|X-3|+|X+2|=6;
(2)解不等式:|X+2|+|X-1|<5.
解 (1)零点为3,-2,分三段讨论.
当X<-2,方程为3-X-(X+2)=6,X=-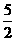 ;
;
当-2≤X≤3,方程为3-X+X+2=6,5=6,无解;
当X>3,方程为X-3+X+2=6,X=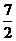 .
.
∴方程的解集为{-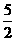 ,
, 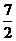 }.
}.
(2)当X<-2,不等式为(1-X)-(X+2)<5,X>-3,∴-3<X<-2;
当-2≤X≤1,不等式为(1-X)+(X+2)<5,3<5,∴-2≤X≤1;
当X>1,不等式为(X-1)+(X+2)<5,X<2,
∴1<X<2.
∴不等式的解集为{X|-3<X<2}.
评析 ①所谓“零点”,即使绝对值为零的X的值.若有n个零点,则分n+1个情况讨论.由于在每区间内可以去掉绝对值符号,就把含有绝对值的方程或不等式转化为普通的方程或不等式去解.
②在每一区间中求方程或不等式的解时,所求得的解必须在这个区间中.
③上面的解法是含有绝对值的问题的基本方法,这两题也可以从绝对值的几何意义直接得到它们的解.
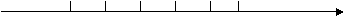
-2 -1 0 1 2 3 x
解 |X-3|+|X+2|=6,即求数轴上到3和-2的对应点距离和等于6的点所对应的数.由数轴知,3-(-2)=5,所以该点在3对应点的右边或在-2对应点左边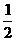 个单位,即X=3
个单位,即X=3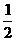 或X=-2
或X=-2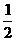 .
.
解 |X -1|+|X+2|<5,即求数轴上到1和-2对应点距离和小于5的点所对应数的范围.由数轴知,1-(-2)=3,所以X应满足-3<X<2.

-2 -1 0 1 2 3 x
3.一元二次不等式
(1)一元二次方程aX2+bX+c=0(a≠0)解的符号情况:
方程有两个正根
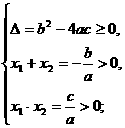
方程有两个负根
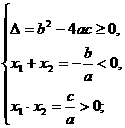
方程有一个正根一个负根 X1·X2=
X1·X2=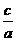 <0(此时必有Δ>0).
<0(此时必有Δ>0).
(2)一元二次不等式.只要熟练掌握相应的抛物线与X轴位置关系,就能迅速准确地求得不等式的解.对于不等式aX2+bX+c>0(<0),实际上就是要求抛物线y=aX2+bX+c在X轴上方(下方)的点的横坐标的范围.
借助于图象,把一元二次不等式的解的情况列表如下(设a>0):
|
Δ的情况 |
图象 |
不等式 |
不等式的解 |
|
|
Δ>0 |
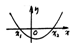 |
ax2+bX+c>0 |
X<X1或X>X2 |
|
|
ax2+bX+c<0 |
X1<X<X2 |
|||
|
Δ=0 |
 |
ax2+bX+c>0 |
X≠X1 |
|
|
ax2+bX+c<0 |
X∈Æ |
|||
|
Δ<0 |
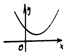 |
ax2+bX+c>0 |
X∈R |
|
|
ax2+bX+c<0 |
X∈Æ |
对于含有等号的不等式或a<0的情况,类似地可以由图象得出不等式的解.但习惯上解一元二次不等式时,常使二次项系数a>0.
例8 已知关于X的方程(k-1)X2+(k+1)X+k+1=0有两个相异实根,求实数k的取值范围.
解 由题设,得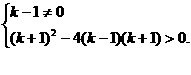
由②,(k+1)(k+1-4k+4)>0,-1<k< .
.
∴实数k的取值范围为-1<k< ,且k≠1.
,且k≠1.
评析 ①两个“相异”实数根即两个不等的实数根,不同于两个“异号”实数根.
② 当二次项系数含有字母时,要注意仅当二次项系数不等于零时方程才有判别式.
例9 已知m、n是关于X的方程X2-2X+t=0的两个实数根。m3+n3有没有最大或最小值?如有请求出最值;如没有,请说明理由.
解 ∵Δ=(-2)2-4·1·t≥0, ∴t≤1,
由韦达定理,m+n=2,mn=t
m3+n3=(m+n)[(m+n)2-3mn]
=2·(22-3t)
=8-6t
≥8-6×1=2.
∴m3+n3的最小值为2,无最大值.
评析 题中“两个实数根”是通常所说的隐含条件,它实际上暗示我们不要遗漏判别式大于或等于零的条件,在审题时一定要引起注意.
例10 解不等式:(1)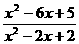 ≤0;(2)
≤0;(2) 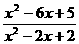 ≤1;
≤1;
(3) 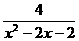 >-1.
>-1.
解 (1)∵X2-2X+2=(X-1)2+1>0,
∴原不等式与不等式X2-6X+5≤0同解.
∴原不等式的解为1≤X≤5.
(2) 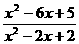 -1≤0,
-1≤0,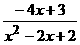 ≤0.
≤0.
∵X2-2X+2>0,∴-4X+3≤0.
∴原不等式的解为X≥ .
.
(3)由 >0,得
>0,得 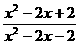 >0.
>0.
∵X2-2X+2>0,∴X2-2X-2>0.
∴原不等式的解为X<1-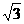 或X>1+
或X>1+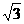 .
.
评析 上面(2)、(3)两题都是采用“移项”、“通分”的方法解分式不等式,这是解分式不等式的基本方法.当分母的符号不能确定时,千万不能用两边同乘以分母的方法去分母,因为若分母为正,去分母后不等号方向不变,若分母为负,去分母后不等号要改变方向.如(3),若两边同乘以分母X2-2X-2,把不等式变成4>-X2+2X+2,即X2-2X+2>0 ①,不等式①的解集为R,显然原不等式的解集{X|X<1-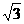 ,或X>1+
,或X>1+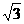 }
} R,两个不等式不同解.当然,假如分母的符号可以确定的话,还是可以去分母的。如题(2),因X2-2X+2>0,两边同乘以X2-2X+2,原不等式变形为X2-6X+5≤X2-2X+2,解为X≥
R,两个不等式不同解.当然,假如分母的符号可以确定的话,还是可以去分母的。如题(2),因X2-2X+2>0,两边同乘以X2-2X+2,原不等式变形为X2-6X+5≤X2-2X+2,解为X≥ ,与原不等式同解.
,与原不等式同解.
练习2
2.|aX+b|<c,|aX+b|>c型不等式
(1)设f(X)=aX+b,一般地,有如下结论:
①当c>0时,|f(X)|<c的解为-c<f(X)<c,|f(X)|>c的解为f(X)<-c或f(X)>c
②当c=0时,|f(X)|<c无解,|f(X)|>c的解即f(X)≠0的解.
③当c<0时,|f(X)|<c无解,|f(X)|>c的解是全体实数.
例5 求满足|2X-1|=|3X+4|的X的值.
解 由绝对值的定义,2X-1=3X+4或2X-1=-(3X-4),∴X=-5或X=-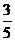 .
.
例6 求下列不等式的解集:
(1)2<|3X-1|≤5;(2)|2X+1|≤t2+3(t∈R).
解 ①不等式的解即不等式组的解:
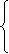
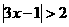
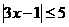
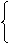
 3x-1<-2或3x-1>2
3x-1<-2或3x-1>2
-5≤3x-1≤5
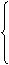 3<-
3<-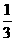 或x>1
或x>1
-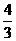 ≤x≤2
≤x≤2
∴不等式的解集为{X|≤-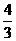 ≤X<-
≤X<-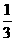 ,或1<X≤2}.
,或1<X≤2}.
②∵t∈R,∴t2+3>0.
1.补集
(1)全集?全集是一个相对的概念,它含有与所研究的问题有关的各集合的全部
元素.在研究不同问题时,全集也不一定相同.
(2)补集?必须注意, 是对于给定的全集I而言的,在不同的问题中全集可能不同,
是对于给定的全集I而言的,在不同的问题中全集可能不同, 也可能不同.如A={1,2},当I={1,2,3,4}时,
也可能不同.如A={1,2},当I={1,2,3,4}时, ={3,4};当I={1,2,3,4,5,6,7,8}时,
={3,4};当I={1,2,3,4,5,6,7,8}时, ={3,4,5,6,7,8}.
={3,4,5,6,7,8}.
例1 已知I=R,A={X|1<X≤3},求 , A∪
, A∪ ,A∩
,A∩
解  ={X|X≤1,或X>3}.
={X|X≤1,或X>3}.
A∪ ={X|1<X≤3}∪{X|X≤1,或X>3}=R=I,
={X|1<X≤3}∪{X|X≤1,或X>3}=R=I,
A∩ ={X|1<X≤3}∩{X|X≤1,或X>3}=Æ.
={X|1<X≤3}∩{X|X≤1,或X>3}=Æ.
说明 在开始学习解这类题时,应画出数轴并借助于数轴求解,否则容易出错.
例 2 已知I={1,2,3,4,5,6},A={3,4,5},B={4,5,6},求 ,
,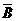 ,
, ∪
∪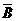 ,A∩B,?
,A∩B,?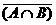 .
.
解  ={1,2,6},
={1,2,6}, 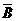 ={1,2,3},
={1,2,3}, ∪
∪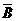 {1,2,3,6},
{1,2,3,6},
A∩B={4,5},?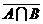 ={1,2,3,6}.
={1,2,3,6}.
评析 由例2,有(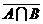 )=
)= ∪
∪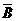 .可以通过韦恩图验证,这个等式对任意的集合A、B、I都能成立.
.可以通过韦恩图验证,这个等式对任意的集合A、B、I都能成立.
例3 已知I=R,A={X|X≥3},B={X|X≤1},求 ,
,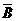 ,
, ∪
∪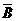 ,
,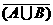
 .
.
解  ={X|X<3},
={X|X<3}, 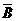 ={X|X>1},
={X|X>1},
 ∩
∩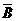 ={X|1<X<3},
={X|1<X<3},
A∪B={X|X≤1或X≥3},
( )={X|1<X<3}.
)={X|1<X<3}.
评析 由例3,有( )=
)= ∩
∩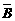 ,可以通过韦恩图验证,这个等式对任
,可以通过韦恩图验证,这个等式对任
意的集合A、B、I都能成立.
例4 用n(A)表示有限集A的元素的个数.
(1)已知n(A)=20,n(B)=15,n(A∪B)=28,求n(A∩B); A B

 (2)已知n(A∩B)=4,n(A∪B)=18,n(A)=10,求n(B)
(2)已知n(A∩B)=4,n(A∪B)=18,n(A)=10,求n(B)
解(1)设n(A∩B)=X,由韦恩图, 20-x x 15-x
∵n(A∪B)=28,
∴(20-X)+X+(15-X)=28,
∴X=7,即n(A∩B)=7. A B
 (2)设集合B中不属于A的无素有X个.
(2)设集合B中不属于A的无素有X个.
由韦恩图,及n(A∪B)=18, 10-4=6 4 x
10+X=18,∴X=8.
∴n(B)=4+8=12.
评析 可以用韦恩图验证,一般地有n(A∪B)=n(A)+n(B)-n(A∩B).但不必硬记这个式子,在涉及到有限集的元素个数时,通常只要适当地设未知数,然后利用韦恩图及已知条件,就可以求得结果.
1.并集.2.|aX+b|<C,|aX+b|>C型不等式.3?一元二次不等式.
1.(代数)2-1.4(P13-26)
21、(16分)已知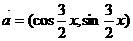 ,
,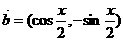 ,且
,且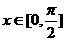 ,求:
,求:
(1)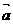 ·
·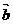 及
及 ;
;
(2) 的最小值为-
的最小值为- ,求实数
,求实数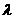 的值.
的值.
20、(16分)求与圆C: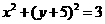 相切,且在
相切,且在 轴、
轴、 轴上的截距相等的直线方程。
轴上的截距相等的直线方程。
19、 (15分)如图:正三角形ABC与直角三角形BCD所在平面互相垂直,且
(15分)如图:正三角形ABC与直角三角形BCD所在平面互相垂直,且
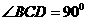 ,
,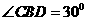
(1)求证: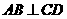 ;
;
(2)求二面角 的正切值.
的正切值.
|
座位号 |
|
18、(14分) 在5件产品中,有3件一等品,2件二等品,从中任取2件,求:(1)恰有1件一等品的概率;
(2)至少有1件一等品的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com