
题目列表(包括答案和解析)
2.若cos(α- ) =
) = , 则cos(
, 则cos( + α)= ( )
+ α)= ( )
(A)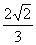 (B)
(B)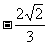 (C)
(C) (D)
(D)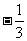
1.已知θ是第二象限角,且满足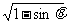 = cos
= cos - sin
- sin , 则
, 则 是 ( )
是 ( )
(A)第四象限角 (B)第三象限角
(C)第二象限角 (D)第一象限角
19. 下表是芝加哥1951-1981年月平均气温(华氏):
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
平均气温 |
21.0 |
26.0 |
36.0 |
48.8 |
59.1 |
68.6 |
73.0 |
71.9 |
64.7 |
53.5 |
39.8 |
27.7 |
(1)以月份为x轴,x=月份-1,以平均气温为y轴,描出散点图,并用一个函数模型近似地描述y与x之间的函数关系.
(2)某蔬菜的种植,要求每月的平均气温不低于60华氏,试确定蔬菜在一年内种植的最长时间.
解:(1)作出的散点图如图所示. 根据图形,可选择正弦曲线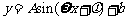 进行拟合.
进行拟合.
 易知,
易知, ,T=12,
,T=12,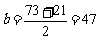 .
.
则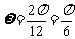 ,
,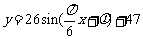
把x=0代入,得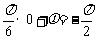 ,即
,即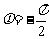 .
.
所以,拟合的函数模型为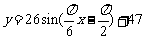 .
.
(2)由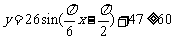 ,即
,即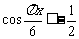 ,解得
,解得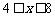 .
.
所以,该蔬菜在一年内种植的最长时间为5个月.
18.设向量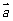 =(sinx,cosx),
=(sinx,cosx),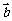 =(cosx,cosx),x∈R,函数f(x)=
=(cosx,cosx),x∈R,函数f(x)= .
.
(1)求函数f(x)的最大值与最小正周期;
(2)求使不等式f(x)≥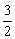 成立的x的取值集合.
成立的x的取值集合.
解:(06年湖北卷.文16)
(1)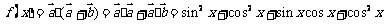
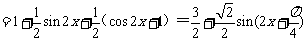
∴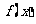 的最大值为
的最大值为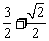 ,最小正周期是
,最小正周期是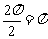 .
.
(2)由(1)知
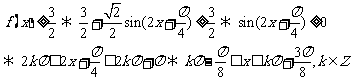
即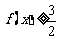 成立的
成立的 的取值集合是
的取值集合是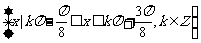 .
.
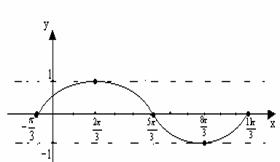
17. 已知函数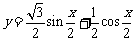 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由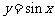 上的图象经怎样的变换得到;
上的图象经怎样的变换得到;
(3)由图象指出函数的单调递减区间、对称轴方程和对称中心点坐标.
解:(1)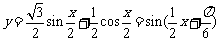 .
.
 最小正周期
最小正周期 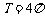
先列表,后描点并画图
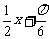 |
0 |
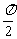 |
π |
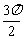 |
2π |
|
x |
 |
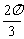 |
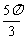 |
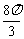 |
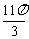 |
|
y |
0 |
1 |
0 |
-1 |
0 |
(2)把y=sinx的图象上所有的点向左平移 个单位长度,得到
个单位长度,得到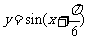 的图象,再把所得图象的横坐标伸长到原来的2倍(纵坐标不变),得到
的图象,再把所得图象的横坐标伸长到原来的2倍(纵坐标不变),得到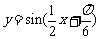 的图象.
的图象.
或把y=sinx的图象横坐标伸长到原来的2倍(纵坐标不变),得到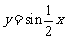 的图象. 再把所得图象上所有的点向左平移
的图象. 再把所得图象上所有的点向左平移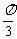 个单位长度,得到
个单位长度,得到 ,即
,即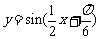 的图象.
的图象.
(3)单调递减区间为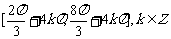 ;
;
对称轴方程为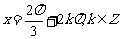 ;对称中心点坐标为
;对称中心点坐标为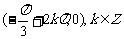 .
.
16. (1)有10本不同的语文书,2本不同的数学书,现从中任意取出2本,能取到数学书的概率有多大?
(1)有10本不同的语文书,2本不同的数学书,现从中任意取出2本,能取到数学书的概率有多大?
(2)如图,在边长为25cm的正方形ABCD中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
解:(1)基本事件的总数为:12×11÷2=66,
“能取到数学书”这个事件所包含的基本事件个数分两种情况:
(i)“恰好取出1本数学书”所包含的基本事件个数为:10×2=20
(ii)“取出2本都是数学书”所包含的基本事件个数为:1
所以“能取到数学书”这个事件所包含的基本事件个数为:20+1=21
因此, P(“能取到数学书”)=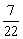
(2)因为均匀的粒子落在正方形内任何一点是等可能的,所以符合几何概型的条件.
设A=“粒子落在中间带形区域”则依题意得:
正方形面积为:25×25=625,
两个等腰直角三角形的面积为:2×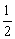 ×23×23=529,
×23×23=529,
带形区域的面积为:625-529=96.
∴ P(A)=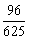 .
.
15. 已知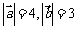 ,
,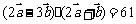 ,
,
(1)求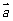 与
与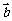 的夹角
的夹角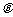 ;
;
(2)若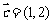 ,且
,且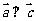 ,试求
,试求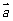 .
.
解:(1)∵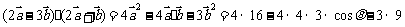 =61,
=61,
∴ 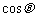 =
= ,
,
∴ 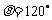 .
.
(2)设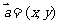 ,则
,则
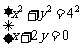 ,解得
,解得 或
或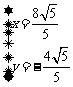 .
.
所以,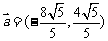 或
或 .
.
14. 规定运算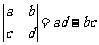 ,若
,若 ,则
,则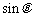 = .
= .
答案: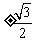
简解: ,则
,则
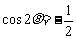 ,又
,又 ,则
,则 .
.
13. 某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 . (用分数作答)
答案: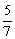
简解:(04年广东卷.13)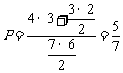
12. 已知向量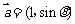 ,
,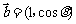 ,则
,则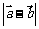 的最大值为 .
的最大值为 .
答案: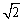
简解:(06年江西卷.文13)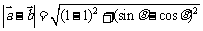 =|sinq-cosq|=
=|sinq-cosq|=
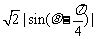 £
£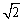
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com