1．算法的定义：

一般地，对一类问题机械的、统一的求解方法称为算法.

例1 写出求1×2×3×4×5的算法.

解 S1：先求1×2，得到结果2；

S2：将步骤1得到的结果2再乘以3，得到6；

S3：将步骤2得到的结果6再乘以4，得到结果24；

S4：将步骤3得到的结果24再乘以5，得到120。

另解^※ S1 让S=1，I=1；

S2 将S×I的值赋给S，I的值增加1；

S3 如果I比5大,则输出S,否则转第二步.

点评 由于计算机是高速计算的自动机器，实现循环的语句.因此，上述算法2不仅是正确的，而且是在计算机上能够实现的较好的算法。在上面的算法中，S2，S3构成一个完整的循环，这里需要说明的是，每经过一次循环之后，变量S、I的值都发生了变化，并且循环一次之后都要在S3对I的值进行检验，一旦发现I的值大于5时，立即停止循环，同时输出最后一个S的值，对于循环结构的详细情况，我们将在以后的学习中介绍。

例2 写出一个求整数a、b、c最大值的算法.

解 S1 先假定序列中的第一个数为"最大值"。

S2 将序列中的下一个整数值与"最大值"比较，如果大于"最大值"，这时就假定这个数为"最大值".

S3 如果序列中还有其它整数，重复S2.

S4 直到序列中没有可比的数为止，这时假定的"最大值"就是序列的最大值.

或写成：

S1 max=a；

S2 如果b>max，则max=b；

S3 如果c>max，则max=c；

S4 max就是a、b、c的最大值.

通过对以上几个问题的分析，我们对算法有了一个初步的了解.在解决某些问题时，需要设计出一系列可操作或可计算的步骤，通过实施这些步骤来解决问题，通常把这些步骤称为解决这些问题的算法.

在数学中，现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成.

问题：我们要解决解决一类问题，我们可以抽象出其解题步骤或计算序列，他们有什么样的要求？

(1)算法与一般意义上具体问题的解法既有联系，又有区别，它们之间是一般和特殊的关系，也是抽象与具体的关系。算法的获得要借助一般意义上具体问题的求解方法，而任何一个具体问题都可以利用这类问题的一般算法来解决。

(2)算法的五个特征

①有限性：一个算法的步骤序列是有限的，它应在有限步操作之后停止，而不能是无限地执行下去；

②确定性：算法中的每一步应该是确定的并且能有效地执行且得到确定的结果，而不应当是模棱两可的；

③逻辑性：算法从初始步骤开始，分为若干个明确的步骤，前一步是后一步的前提，只有执行完前一步才能进行下一步，并且每一步都准确无误，才能完成问题；

④不唯一性：求解某一个问题的算法不一定只有唯一的一个，可以有不同的算法；

⑤普遍性：很多具体的问题，都可以设计合理的算法去解决，如心算、计算器计算都要经过有限的、事先设计好的步骤加以解决.

广义地说为了解决某一问题而采取的方法和步骤，就称之为算法。做任何事情都有一定的步骤。例如：描述太极拳动作的图解，就是“太极拳的算法”；一首歌的乐谱，可以称之为该歌曲的算法.从小学到高中遇到的算法绝大多数都与“计算”有关的问题。

问题4　 给出求1+2+3+4+5的一个算法.

解(算法1)：按照逐一相加的程序进行：

　　 第一步：计算1+2，得到3；

第二步：将第一步中的运算结果3与3相加，得到6；

　　 第三步：将第二步中的运算结果6与4相加，得到10；

　　 第四步：将第三步中的运算结果10与5相加，得到15.

　　 解(算法2)可以运用公式1+2+3+…+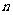=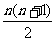直接计算：

　　 第一步：取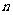=5；

第二步：计算；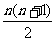

　　 第三步：输出运算结果.

解(算法3)按照累积相加的程序进行：

第一步：让S=0，I=1　

第二步：将S+I的值赋给S，I的值增加1

第三步：如果I比5大,则输出S,否则转第二步.

(说明算法不唯一)

解：S1　 ②-①×2得3y=-3；③

　　 S2　 解③得y=-1；

　　 3S　 将y=-1代入①，得x=4.

对于一般的二元一次方程组来说，上述步骤是否具有一般性？应该怎样进一步完善？

点评：本题的算法是由加减消元法求解的，为了使这个算法适合一般的二元一次方程组的解，可以改为：

S1　 方程①不动，将方程②中x的系数除以方程①中x的系数，可得乘数；

S2　 方程②减去乘以方程①，消去方程②中的x项，得到；

S3　 将上面的方程组自下而上回代求解，得到y=-1，x=4.

S4　 写出方程组的解.

这种消元回代的算法使用一般线形方程组的求解--说明算法的普遍性.

第一步：②×A₁-①×A₂，得(A₁B₂-A₂B₁)y+A₁C₂-A₂C₁=0；③

第二步：解③，得；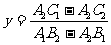

第三步：将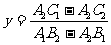代入①，得。

此时我们得到了二元一次方程组的求解公式，利用此公司可得到问题5的另一个算法：

第一步：取A₁=1，B₁=-2，C₁=1，A₂=2，B₂=1，C₂=-1；

第二步：计算与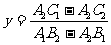

第三步：输出运算结果。

可见利用上述算法，更加有利于上机执行与操作。

问题1：写出你在家里烧开水的过程.

一般地，第一步：把水注入电水壶；第二步：打开电源把水烧开；第三步：把烧开的水注入热水瓶.

问题2：两个大人和两个小孩一起渡河，渡口只有一条小船，每次只能渡1 个大人或两个小孩，他们四人都会划船，但都不会游泳。试问他们怎样渡过河去？请写出一个渡河方案.

(通过学生讨论得出渡河方案与步骤如下)

S1　 两个小孩同船过河去；

S2　 一个小孩划船回来；

S3 　一个大人划船过河去；

S4 　对岸的小孩划船回来；

S5　 两个小孩同船渡过河去；

S6　 一个小孩划船回来；

S7　 余下的一个大人独自划船渡过河去；对岸的小孩划船回来；

S8 　两个小孩再同时划船渡过河去。

问题3 说出解一元一次方程的步骤.

一般地，S1：去分母；S2：去括号；S3：移项；S4：合并同类项；S5：除以一次项的系数，得方程的解.

22．(14分)已知sin(3π-α)=sin(2π+β),cos(-α)= -cos(π+β),且0<α<π,0<β<π,求sinα及sinβ的值.

21．(14分)已知关于x的方程2x²－(+1)x+m＝0的两根为sinθ和cosθ，θ∈(0,2π)，求：

(1) +的值；

(2)m的值；

(3)方程的两根及此时θ的值．

20．(12分)证明: 已知sin²α+5sinα-4sinαcosα-20cosα=0,求下列各式的值．

(1) ;　　 (2) sin²α-3sinαcosα+9cos²α

19．(12分)已知cosα＝m，(|m|≤1)，求sinα，tanα的值．

18．(12分)已知扇形的周长为L，问当扇形的圆心角α和半径R各取何值时，扇形面积最大？