
题目列表(包括答案和解析)
2.已知集合A={0,4},B={0,2},下列从A到B的对应关系为f,x∈A,y∈B,不是映射的是 ( )
A、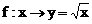 B、
B、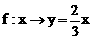
C、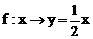 D、
D、
1. 下列关系中正确的个数为
①0∈{0},②Φ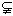 {0},③{0,1}
{0},③{0,1} {(0,1)},④{(a,b)}={(b,a)} (
)
{(0,1)},④{(a,b)}={(b,a)} (
)
A. 1 B. 2 C. 3 D. 4
22.证明:(1)∵  ,
,
∴ 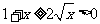 ,
, ,
, ,
,
三式相乘,则有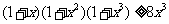 ;
;
(2)当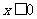 时,
时,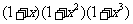
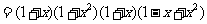
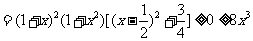 ,
,
∴  ,不等式
,不等式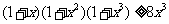 仍成立。
仍成立。
21.解:本题的最终结果是:
|
日期 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
件数 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
|
||||||||||
|
日期 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
件数 |
33 |
36 |
39 |
37 |
35 |
33 |
31 |
29 |
27 |
25 |
|
|
||||||||||
|
日期 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
件数 |
23 |
21 |
19 |
17 |
15 |
13 |
11 |
9 |
7 |
5 |
|
|
||||||||||
|
日期 |
31 |
|
|
|
|
|
|
|
|
|
|
件数 |
3 |
|
|
|
|
|
|
|
|
|
(1)据此可知5月13日最多,是39件;
(2)5月12日(共有234件)开始流行,到5月22日,共11天。
20.解:(Ⅰ)由 ,得
,得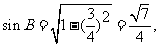
由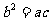 及正弦定理得
及正弦定理得 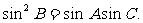
于是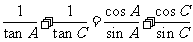
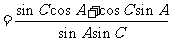
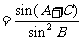

(Ⅱ)由 ,得
,得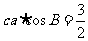 ,由
,由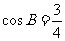 ,可得
,可得 ,即
,即 .
.
由余弦定理 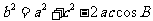 ,得
,得 ,
,
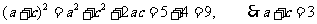 .
.
19.解:如图,设 ,
, ,则
,则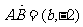 ,
,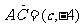 ,
,
依题意有 ,
,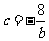
而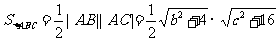

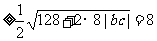 .
.
18.解:设每天派出A型车与B型车各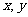 辆,并设公司每天的成本为
辆,并设公司每天的成本为 元.由题意,得
元.由题意,得
 ,且
,且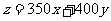 .即
.即
作出可行域,作直线 :
: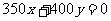 ,即
,即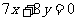 .
.
作出一组平行直线: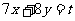 中(
中( 为参数)经过可行域内的点和原点距离最近的直线,此直线经过
为参数)经过可行域内的点和原点距离最近的直线,此直线经过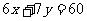 和
和 的交点
的交点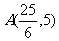 ,由于点A的坐标不都是整数,而
,由于点A的坐标不都是整数,而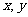
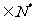 ,所以可行域内的点
,所以可行域内的点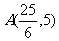 不是最优解.
不是最优解.
为求出最优解,必须进行定量分析.
因为,7× +8×5≈69.2,所以经过可行域内的整点(横坐标和纵坐标都是整数的点)且与原点最小的直线是
+8×5≈69.2,所以经过可行域内的整点(横坐标和纵坐标都是整数的点)且与原点最小的直线是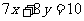 ,在可行域内满足该方程的整数解只有
,在可行域内满足该方程的整数解只有 ,
,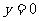 ,
,
所以(10,0)是最优解,即当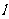 通过B点时,
通过B点时,
 元为最小.
元为最小.
答:每天派出A型车10辆不派B型车,公司所化的成本费最低为3500元.
17.解:设等差数列的公差是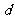 ,等比数列的公比是
,等比数列的公比是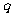 ,则由
,则由
 得:
得:

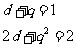 ,解得
,解得
 ,
,
从而数列 的通项公式是
的通项公式是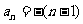 ,数列
,数列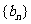 的通项公式
的通项公式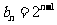
数列 的前
的前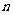 项的和是:
项的和是:

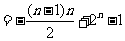 .
.
14.17 15.1 16.1003
11.3
12. 13.24
13.24
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com