
题目列表(包括答案和解析)
6. 集合A={a2,a+1,-1},B={2a-1,| a-2 |, 3a2+4},A∩B={-1},则a的值是( D )
A.-1 B.0 或1 C.2 D.0
5.
满足{1,2,3} 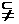 M
M 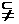 {1,2,3,4,5,6}的集合M的个数是 ( C )
{1,2,3,4,5,6}的集合M的个数是 ( C )
A.8 B.7 C.6 D.5
3.
设集合A={x|1<x<2},B={x|x<a}满足A
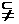 B,则实数a的取值范围是 ( A )
B,则实数a的取值范围是 ( A )
 A.{a|a ≥2} B.{a|a≤1} C.{a|a≥1}. D.{a|a≤2}.
A.{a|a ≥2} B.{a|a≤1} C.{a|a≥1}. D.{a|a≤2}.
2. 如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( B )
A.0 B.0 或1 C.1 D.不能确定
1、已知全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },那么集合 { 2 ,7 ,8}是 ( C )



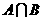

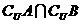

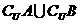
15. 已知向量
 ,
, 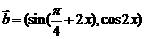 (
(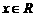 ). 设函数
). 设函数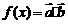 .
.
(1)求 的值; (2)求
的值; (2)求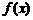 的最大值及对应的
的最大值及对应的 值.
值.
16. 已知
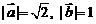 .
.
(1)若 的夹角
的夹角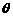 为
为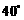 ,求
,求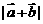 ;(精确到0.001)
;(精确到0.001)
(2)若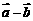 与
与 垂直,求
垂直,求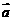 与
与 的夹角
的夹角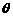 .
.
17. 在一次商贸交易会上,一商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有6个红球和4个白球的袋中无放回地取出2个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在9:00-9:40之间赶到,乙计划在9:20-10:00之间赶到,求甲比乙提前到达的概率.
18. 已知函数
 .
.
(1)画出函数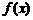 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图;
(2)将函数 的图象作怎样的变换可得到
的图象作怎样的变换可得到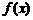 的图象?
的图象?
(3)设函数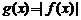 ,求
,求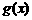 的周期、单调递减区间.
的周期、单调递减区间.

19. 某“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度y(米)随着时间t(0≤t≤24,单位:小时)而周期性变化. 为了了解变化规律,该队观察若干天后,得到每天各时刻t的浪高数据的平均值如下表:
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.9 |
0.4 |
1.0 |
(1)试画出散点图;
(2)观察散点图,从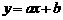 、
、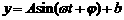 、
、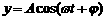 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定当浪高不低于0.8米时才进行训练,试安排白天内进行训练的具体时间段.
14. 由物理中矢量运算及向量坐标表示与运算,我们知道:
(1)两点等分单位圆时有相应关系式为: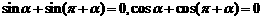 ;
;
(2)四点等分单位圆时有相应关系式为: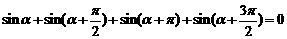 ,
,
 .
.
由此我们可以推测,三点等分单位圆时的相应关系式为 ,
.
13. 某校1000名学生中,O型血有400人,A型血有250人,B型血有250人,AB型血有100人,为了研究血型与性格的关系,按照分层抽样的方法从中抽取样本. 如果从A型血中抽取了10人,则从AB型血中应当抽取的人数为 .
12. 已知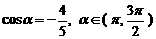 ,则
,则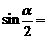 .
.
11. 若向量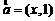 与
与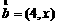 垂直,则
垂直,则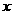 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com