
题目列表(包括答案和解析)
2. 教学例题:
① 出示例1:求下列各角的正弦、余弦、正切值
3π、 -2π、 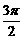 、 -
、 -
讨论求法→试求(学生板演)→订正→小结:画终边与单位圆,求交点,求值.
② 思考:已知角终边上任一点P (x, y),如何求它的三角函数值呢?
结论:先求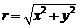 ;再按公式
;再按公式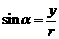 、
、 、
、 .
.
③ 出示例2:已知角α的终边过点P(-2,-4),求α的正弦、余弦和正切值.
(学生试求→订正→小结解法:先求r,再按定义求. )
④ 讨论:正弦、余弦、正切值在各个象限的符号情况?
⑤ 讨论:终边相同的角同一三角函数的值有何关系?
结论:
 ,
, ,
, 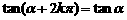 ,其中
,其中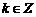 .
.
作用:把任意角的三角函数值问题转化为0-2π间角的三角函数值问题.
⑥ 练习:求下列各角的正弦、余弦和正切值: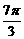 、-
、-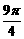 .
.
1. 教学任意角的三角函数的定义:
① 讨论:锐角α的终边交单位圆于点P (x,y)的坐标与α三角函数有何关系?
→ 推广:任意角
② 定义:设α是一个任意大小的角,角α的终边与单位圆交于点P (x, y),
则sinα=y,cosα=x,tanα= .
.
② 讨论:与点P的位置是否有关?
α与2kπ+α的三角函数值有何关系?
当α的终边落在x轴、y轴上时,哪些三角函数值无意义?
任何实数是不是有三角函数值?
三个三角函数的定义域情况是怎样的?
3. 讨论:以上定义适应任意角的三角函数吗?如何定义?
2. 锐角的三角函数如何定义?
1. 用弧度制写出终边在下列位置的角的集合:坐标轴上; 第二、四象限
20.(本题满分10分)我国是水资源比较贫乏的国家之一,各地采用价格调控手段来达到节约用水的目的,某市用水收费的方法是:水费=基本费+超额费+损耗费,若每月用水量不超过最低限量a立方米时,只付基本费8元和每户每月的定额损耗费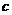 元;若用水量超过最低限量a立方米时,除了付同上的基本费和损耗费外,超过部分每立方米付b元的超额费,已知每户每月的定额损耗费不超过5元.现该市有一家庭今年第一季度的用水量和支付费用如下表所示:
元;若用水量超过最低限量a立方米时,除了付同上的基本费和损耗费外,超过部分每立方米付b元的超额费,已知每户每月的定额损耗费不超过5元.现该市有一家庭今年第一季度的用水量和支付费用如下表所示:
|
月份 |
用水量 |
水费 |
|
1月 |
9 |
9元 |
|
2月 |
15 |
19元 |
|
3月 |
22 |
33元 |
根据该表格中的数据,求出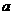 、
、 、
、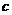 .
.
19.(本题满分12分)定义在R上的函数 ,
,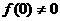 ,当
,当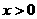 时
时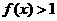 ,且对任意的
,且对任意的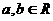 有
有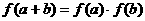
(1)求证: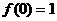 .
.
(2)求证:对任意的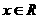 ,恒有
,恒有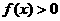 .
.
(3)求证: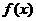 是R上的增函数.
是R上的增函数.
(4)若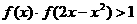 ,求
,求 的取值范围.
的取值范围.
18.(本题满分9分)若 (
(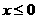 ).求
).求
(1)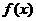 的表达式、定义域和值域.
的表达式、定义域和值域.
(2)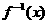 的表达式、定义域和值域.
的表达式、定义域和值域.
17.(本题满分9分)已知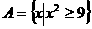 ,
,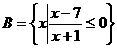 ,
,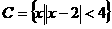
(1)求 及
及
(2)若I=R,求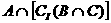
16.已知关于 的函数
的函数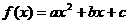 (
(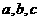 为常数且
为常数且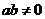 ),若
),若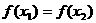 (
( ),则
),则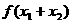 的值等于
.
的值等于
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com