3. 小结：三角函数的符号及诱导公式的运用；利用诱导公式一,可以把求任意角的三角函数值, 转化为0°-360°而求，或用计算器求.

2. 教学诱导公式的运用：

① 讨论：根据三角函数的定义，θ与2kπ+θ的三个三角函数情况怎样？

② 提出：诱导公式一(三个)

　分析作用：求任意角的三角函数转化到0-2π间求值.

③ 出示例：求下列各角的三角函数的值(正弦、余弦、正切).

75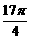0°、、－、－1020°

(教师示例750°→学生试求其它三个→订正)

④ 练习：函数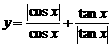的值域.

解法：分象限讨论，去绝对值.

变式：求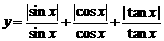的值域.

1. 教学三角函数值的符号：

① 讨论：各个象限的符号情况？

② 出示例：判别下列各三角函数值的符号，然后用计算器验证.

sin250°、cos(－)、tan(－666°36’)、tan、sin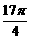、cos1020°

(分析：如何用诱导公式(1)转化到0°-360°？→ 试练 → 订正)

③ 出示例：根据下列已知，判别θ所在象限：

sinθ>0且tanθ<0 、　　　 tanθ×cosθ<0

(口答→分析思路)

2. 在0-2π或0°-360°间求出与下列终边相同的角：

75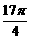0°、、－、－1020°

1. 提问：三个三角函数的定义、定义域及在各个象限的符号情况怎样？(填表形式)

4. 作业：书P17　 1、2、3题.

第二课时：1.2.1　 任意角的三角函数(二)

教学要求：掌握三角函数的符号，灵活运用诱导公式(一)，把求任意角的三角函数值转化为求0°-360°间的三角函数值.

教学重点：灵活运用诱导公式.

教学难点：理解转化.

教学过程：

3. 已知点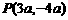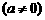，在角α的终边上，求、、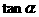的值

2. 口答下列各特殊角的正弦、余弦、正切值：0°、90°、180°、270°、360°.

1. 已知角α的终边在直线y＝2x上，求α的正弦、余弦和正切值.

3. 小结：单位圆定义任意角的三角函数；由终边上任一点求任意角的三角函数；各象限的符号情况；诱导公式(一).