1. 作、、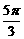－40°的正弦线、余弦线、正切线.

4. 小结：三角函数线概念与作法；三角函数线的运用.

3. 教学例题：

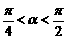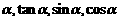① 出示例：已知，试比较的大小.

　 (分析：如何通过三角函数线比较？ → 小结：利用三角函数线比大小 → 变式：)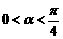

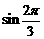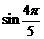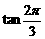② 练习：利用三角函数线比较下列各组数的大小：与；与.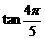

2. 讨论问题：

① 讨论一：三角函数线为什么可以表示三角函数值？

　先单位圆中计算得sinα=y，cosα＝x；

　比较MP的长度与|y|、OM的长度与|x|；

　比较MP的符号与y的符号，OM的符号与x的符号；

所以 sinα＝y＝MP，　 cosα＝x＝OM，

　tanα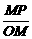＝＝=＝AT 　(由三角形相似得)

② 讨论二：α终边在坐标轴上时的正弦线、余弦线、正切线的情况？

1. 教学三角函数线概念：

① 定义有向线段：直线规定方向→轴；线段规定方向→有向线段；

② 讨论有向线段表示：与轴正向同为正，否则为负.

③ 练习：如图，AB＝　 BA＝　 OC＝　　 CD＝　 DC＝

④ 画出下列角度与单位圆的交点P，并作x轴的垂线PM，写出PM、OM的值，并与正弦、余弦值比较：　 120°、240°

⑤ 定义正余弦线：设角α的终边与单位圆交点P(x，y),过P作x轴的垂线，垂足为M，则有向线段MP为正弦线，OM为余弦线.

⑥ 练习：画出各象限终边角的正弦线、余弦线，并分析符号.

⑦ 定义正切线：过点A(1,0)作单位圆的切线，与终边或延长线交于T，则有向线段AT叫角α的正切线. 　

⑧ 练习：画出各象限终边角的正切线，并分析符号.

2. 三个三角函数是怎样定义的？

D　　 y 　 C　　　 A　 B 　　　　　　　　 x

1. 什么叫单位圆？(以原点为圆心，单位长为半径作的圆)

3. 作业：教材P17　 5、7题.

第三课时：用单位圆中的线段表示三角函数值

教学要求：理解正弦线、余弦线、正切线的概念，掌握作已知角α的正弦线、余弦线和正切线.

教学重点：掌握作已知角α的正弦线、余弦线、正切线.

教学难点：理解正弦线、余弦线、正切线的概念.

教学过程：

2. 解方程：|sinx|＝－sinx

　　 (思路：根据各象限的符号，分情况讨论)

1. 已知θ∈(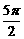,3π)，求：

3+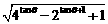的值.