
题目列表(包括答案和解析)
4. 作业:教材P24 11、12、13题.
3. 已知tanα=2,求下列各式的值: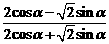 ;
;  .
.
2. 已知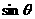 =
= ,求
,求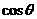 和
和 的值.
的值.
1. 已知α是第二象限角,且tan(2π+α)=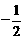 , 求cosα和sinα的值.
, 求cosα和sinα的值.
3. 小结:注意象限定符号和联系关系式. 灵活运用公式,注意平方关系,切化弦;化繁为简.
2. 练习:
① 已知sin =2sinβ,tan
=2sinβ,tan =3tanβ,求
=3tanβ,求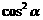 的值.
的值.
② 已知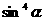 +
+ =1,求sinα+cosα的值.
=1,求sinα+cosα的值.
1. 教学例题:
① 出示例1:用多种方法证明: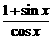 =
=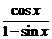
学生讨论证法,逐一补充完整
证法一: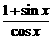 =
=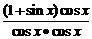 =…
=…
证法二: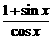 =
=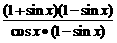 =…
=…
证法三、四:从右边开始,……
证法五:(1+sinx)(1-sinx)=…
② 小结方法:由其它等式而转化(先证交叉乘积相等);或证和(差),或证商→比较法;直接证明左边等于右边.
③ 练习:求证:sin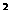 x tan
x tan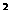 x =tan
x =tan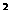 x-sin
x-sin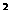 x.
x.
④ 出示例2:已知tanα=-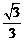 ,求α的其它三角函数的值;求
,求α的其它三角函数的值;求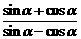 的值.
的值.
分析:如何运用同角三角函数基本关系式求解?
变式:如何直接求第2问? (弦化切)
训练: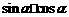 (技巧:切用分母1)
(技巧:切用分母1)
2. 提问:同一个角的三个三角函数有哪些基本关系式?
1. 根据下列条件,求角α的其它三角函数值.:sinα=- ,α在第四象限; tanα=2
,α在第四象限; tanα=2
3. 作业:教材P23 练习1、2、4题.
第五课时:1.2.2 同角三角函数的基本关系(2)
教学要求:能熟练运用同角三角函数的三个基本关系式,掌握已知一个角的某一个三角函数值,求这个角的其它三角函数值;能利用关系式化简三角函数式. 能够利用三角函数的基本关系式证明有关的三角恒等式.
教学重点:运用公式.
教学难点:合理选用关系式.
教学过程:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com