
题目列表(包括答案和解析)
4. 作业:书P125 2.
第二课时:2.5.2 向量在物理中的应用举例
教学要求:理解向量线性运算及数量积运算,会用向量知识解决物理问题.
教学重点:理解并能灵活应用向量线性运算及数量积的意义和性质.
教学难点:理解并能灵活应用向量线性运算及数量积的意义和性质.
教学过程:
3.
在平行四边形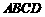 中,已知
中,已知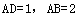 ,对角线
,对角线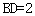 ,求对角线
,求对角线 的长.
的长.
2. 求证:两条对角线互相垂直平分的四边形是菱形.
1.
已知平行四边形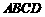 ,
,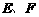 在对角线
在对角线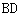 上,并且
上,并且 ,求证
,求证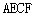 是平行四边形.
是平行四边形.
3. 小结:向量加减法与向量数量积的运算法则;向量加减法与向量数量积的意义和性质.
1. 教学平面几何的向量:
教学平面几何的向量:
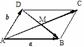
① 平移、全等、相似、长度、夹角等几何性质可以由向量线性运算及数量积表示出来例如,向量数量积对应着几何中的长度.如图: 平行四边行 中,设
中,设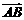 =
=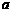 ,
,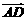 =
=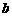 ,则
,则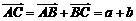 (平移),
(平移),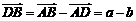 ,
, (长度).向量
(长度).向量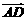 ,
,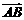 的夹角为
的夹角为
② 讨论:(1)向量运算与几何中的结论"若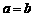 ,则
,则 ,且
,且 所在直线平行或重合"相类比,你有什么体会?(2)由学生举出几个具有线性运算的几何实例.
所在直线平行或重合"相类比,你有什么体会?(2)由学生举出几个具有线性运算的几何实例.
③ 用向量方法解平面几何问题的步骤(一般步骤)
(1) 建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量.
(2) 通过向量运算研究几何运算之间的关系,如距离、夹角等.
(3) 把运算结果"翻译"成几何关系.
2.讨论:① 若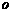 为
为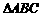 的重心,则
的重心,则 +
+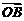 +
+ =0
=0
②水渠横断面是四边形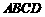 ,
, =
=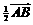 ,且
,且 |=
|=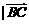 |,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?
|,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?
1.提问:向量的加减运算和数量积运算是怎样的?
21.(14分)是否存在α.β,α∈(-,),β∈(0,π),使等式sin(3π-α)=cos(-β),cos(-α)=-cos(π+β)同时成立?若存在,求出α,β的值,若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com