
题目列表(包括答案和解析)
3.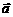 为非零向量,试求
为非零向量,试求 和
和 的值.
的值.
2.如图: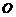 是正方形
是正方形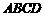 的中心,求下列各式的值
的中心,求下列各式的值
①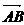 +
+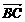 ②
②  -
-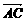
1. 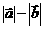 与
与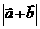 、
、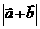 与
与 有何关系?什么时候等号成立?
有何关系?什么时候等号成立?
3.作业:93页第1、2题.
第二课时 2.2. 3 向量数乘运算及其几何意义
教学要求:理解向量的数乘运算及其几何意义,会进行向量的数乘运算.
教学重点:向量的数乘运算
教学难点:向量的数乘运算的几何意义
教学过程:
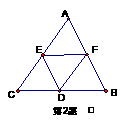
2.如图,D、E、F分别为三边的中点,试画出 -
-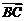 、
、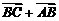 、
、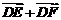
1.如右图,画出 .
.
2. 教学例题:
① 课本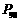 例1、
例1、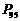 例3,
例3,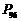 例4.
例4.
(师生共同完成,注意两种法则的区别,然后变式--加变减、减变加)
② 练习:课本93页第1、2题.
③ 讨论: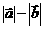 与
与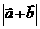 、
、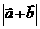 与
与 有何关系.
有何关系.
④ 用三角形法则、平行四边形法则探讨向量的加减运算是否满足交换律、结合律.
 ⑤
⑤  例2. (向量的实际应用,师生共同完成;变式:若船行走的路线是垂直于河岸,求速度)
例2. (向量的实际应用,师生共同完成;变式:若船行走的路线是垂直于河岸,求速度)
1. 教学向量的加(减)法运算:
① 向量的加(减)法:求两向量和(差)的运算叫向量的加(减)法运算
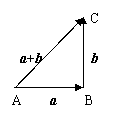 ② 三角形法则:向量
② 三角形法则:向量 与
与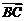 相加时,
相加时, 的终点B作为
的终点B作为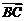 的起点,这时起点A到终点C的向量
的起点,这时起点A到终点C的向量 就是这两个向量的和向量,即
就是这两个向量的和向量,即

 . 这种求向量和的方法叫三角形法则. (
. 这种求向量和的方法叫三角形法则. (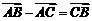 )
)
(注意:两个向量要“首尾”相接)
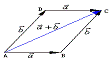
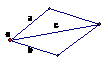
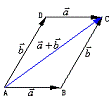 ③平行四边形法则:由同一点A为起点的两个已知向量
③平行四边形法则:由同一点A为起点的两个已知向量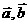 为邻边作平行四边形ABCD,则以A为起点的向量
为邻边作平行四边形ABCD,则以A为起点的向量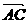 就是向量
就是向量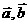 的和. 这种作两个向量和的方法叫做平行四边形法则,如右图:
的和. 这种作两个向量和的方法叫做平行四边形法则,如右图:
④讨论:三角形法则、平行四边形法则是否对所有向量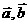 求和都适用?
求和都适用?
(注意:平行四边形法则对于两个向量共线时不适用. )
⑤定义相反向量:与向量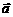 的长度相等、方向相反的向量叫做向量
的长度相等、方向相反的向量叫做向量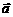 的相反向量,记作:
的相反向量,记作: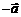
规定零向量的相反向量仍是零向量.
注:向量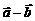 可以看成是
可以看成是
3. 回顾思考:力是向量,如何求
回顾思考:力是向量,如何求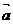 、
、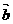 这两个力的合力呢?用什么方法?
这两个力的合力呢?用什么方法?
2.如图: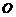 是正方形
是正方形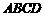 的中心,①向量
的中心,①向量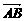 与
与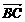 相等吗?
相等吗?
② 向量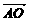 与
与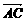 是平行向量吗? ③ 求
是平行向量吗? ③ 求 :
: 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com