
题目列表(包括答案和解析)
2.向量的加、减、数乘运算统称为向量的线性运算.
1. 回顾向量、零向量、单位向量、平行向量、、共线向量、相反向量相等向量是如何定义的.
(是否是零向量、单位向量只需判断长度,要判断是否为相等向量、共线向量、相反向量则还要看方向)
5.作业:课本第100页第4、5题.
第三课时 2.2. 3 向量的相关概念及向量线性运算(练习)
教学要求:掌握向量的相关概念,能熟练进行向量的线性运算.
教学重点:向量的线性运算,掌握向量运算的几何作图.
教学难点:向量的线性运算.
教学过程:
4.在三角形ABC中, ,
,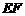 ∥
∥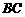 交AC于F点,试用
交AC于F点,试用 、
、 表示
表示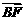 .
.
3.求证:M是线段AB的中点,对于任意一点O,都有
2. 已知向量,求作向量 ,使
,使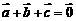 ,表示的有向线段能构成三角形吗?
,表示的有向线段能构成三角形吗?
1. 计算:(1) (2)
(2)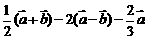
3.小结:向量的数乘运算;两向量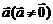 与
与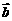 共线满足
共线满足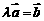
2、教学例题:
① 例5:计算:⑴ ⑵
⑵  ⑶
⑶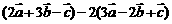
(去括号,实数与实数运算后再与向量运算)
② 定理:向量 与
与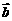 共线(
共线( ),当且仅当有唯一一个实数
),当且仅当有唯一一个实数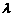 ,使
,使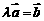 .
.
 ③ 出示例题6:(分析:三点可分共线与不共线两种情形,可以通过判断以这三点为端点的向 量是否共线来判断点是否共线)
③ 出示例题6:(分析:三点可分共线与不共线两种情形,可以通过判断以这三点为端点的向 量是否共线来判断点是否共线)
④ 定义线性运算:向量的加、减、数乘运算统称为向量的线性运算.
⑤ 出示例题7. (先找出与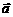 、
、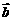 向量共线的向量,再利用定理)
向量共线的向量,再利用定理)
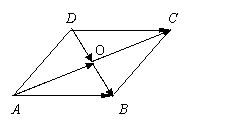
⑥ 练习:如图,试用向量方法证明:对角线互相平分的四
边形是平行四边形
1. 教学向量的数乘运算:
①
向量的数乘:求实数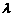 与向量
与向量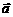 的乘积的运算叫向量的数乘,记作:
的乘积的运算叫向量的数乘,记作: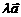
规定:(Ⅰ) 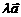 仍然是个向量
(Ⅱ)、
仍然是个向量
(Ⅱ)、
(Ⅲ) 当 时向量
时向量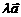 的方向与
的方向与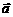 的方向相同,当
的方向相同,当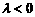 时,向量
时,向量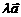 与
与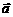 的方向相反,
的方向相反,
当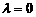 时,
时,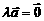
② 练习: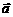 为单位向量,试求
为单位向量,试求 、
、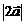 、
、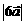 、
、 的值:变式:
的值:变式: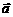 为非零向量.
为非零向量.
③ 讨论验证下列等式: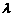 、
、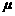 为实数,
为实数,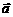 、
、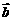 为向量.
为向量.
⑴ 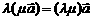 ⑵
⑵ 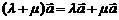 ⑶
⑶ 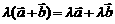
(数乘运算满足交换律、结合律、分配律)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com