2.向量的数量积的几何意义.

1.平面向量的数量积的物理背景及其含义?

5.作业：课本P119　 A组 1，2，3题.

第二课时　 2.4.2平面向量数量积的坐标表示、模、夹角

教学要求：使学生掌握平面向量数量积的坐标表示, 掌握向量垂直的坐标表示的条件，及平面内两点间的距离公式,能用所学知识解决有关综合问题.

教学重点：平面向量数量积的坐标表示的应用.

教学难点：平面向量数量积的坐标表示的综合运用

教学过程：

4．已知a+b=2i-8j，a-b=-8i+16j，其中i、j是直角坐标系中x轴、y轴正方向上的单位向量，那么a·b=？

3．对于两个非零向量a、b，求使|a+tb|最小时的t值，并求此时b与a+tb的夹角.

2．设m、n是两个单位向量，其夹角为60°，求向量a=2m+n与b=2n-3m的夹角.

1．已知|a|=1，|b|=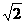，(1)若a∥b，求a·b；(2)若a、b的夹角为60°，求|a+b|；(3)若a-b与a垂直，求a与b的夹角.

3. 小结：1.平面向量数量积(内积)的定义；2.向量的数量积的几何意义.

2.教学例题

①.讲解范例：例1 已知|a|=5， |b|=4， a与b的夹角θ=120^o，求a·b.

例2 已知|a|=6， |b|=4， a与b的夹角为60^o求(a+2b)·(a-3b).

例3 已知|a|=3， |b|=4， 且a与b不共线，k为何值时，向量a+kb与a-kb互相垂直.

(教师演示学生模仿学生演示)

②.练习：已知｜a｜＝3，｜b｜＝6，当①a∥b，②a⊥b，③a与b的夹角是60°时，分别求a·b.

1.教学向量的数量积的概念.

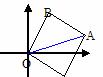
①.两个非零向量夹角的概念：已知非零向量a与b，作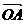＝a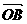，＝b，则∠AOB＝θ(0≤θ≤π)叫a与b的夹角.注意：当θ＝0时a与b同向；当θ＝π时，a与b反向；当θ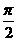＝时，a与b垂直，记a⊥b；

②.平面向量数量积(内积)的定义: 已知两个非零向量a与b，它们的夹角是θ，则数量|a||b|cosq叫a与b的数量积，记作a×b，即有a×b = |a||b|cosq，

　　　　　　 (分析：符号由cosq的符号所决定；两个向量的数量积称为内积，写成a×b；)

③.“投影”的概念：作图定义：|b|cosq叫做向量b在a方向上的投影. 投影也是一个数量，不是向量；当q为锐角时投影为正值；当q为钝角时投影为负值；当q为直角时投影为0；当q = 0°时投影为 |b|；当q = 180°时投影为 -|b|　　　　　　 　

　　　　　　 ④．向量的数量积的几何意义：数量积a×b等于a的长度与b在a方向上投影|b|cosq的乘积.

⑤.性质：e×a = a×e =|a|cosq ，a^b Û a×b = 0，当a与b同向时，a×b = |a||b|；当a与b反向时，a×b = -|a||b|. 特别的a×a = |a|²或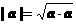 cosq =)

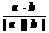⑥探究：运算律 a×b=b.a　 (λa).b=λ(a.b)