
题目列表(包括答案和解析)
6. 已知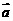 (4,2), 求与
(4,2), 求与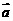 垂直的单位向量的坐标.
垂直的单位向量的坐标.
5.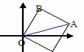 如图,以原点和A(5, 2)为顶点作等腰直角△OAB,使ÐB = 90°,求点B和向量
如图,以原点和A(5, 2)为顶点作等腰直角△OAB,使ÐB = 90°,求点B和向量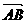 的坐标.
的坐标.
4. 已知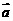 =(1,
=(1,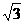 ),
),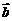 =(
=(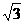 +1,
+1,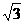 -1),则
-1),则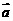 与
与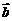 的夹角是多少?
的夹角是多少?
3. 已知A(1,2),B(2,3),C(-2,5),则△ABC为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不等边三角形
2.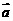 =(2,3),
=(2,3),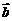 =(-2,4),则(
=(-2,4),则(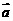 +
+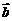 )·(
)·(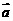 -
-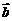 )= .
)= .
1.已知A(3,2),B(-1,-1),若点P(x,-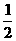 )在线段AB的中垂线上,则x= .
)在线段AB的中垂线上,则x= .
3.小结: 平面内两点间的距离公式;向量垂直的判定;两向量夹角的余弦.
2.教学例题.
① 讲解例5:已知A(1, 2),B(2, 3),C(-2, 5),试判断△ABC的形状,并给出证明
练习:在△ABC中,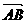 =(2,
3),
=(2,
3),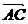 =(1, k),且△ABC的一个内角为直角,求k值.
=(1, k),且△ABC的一个内角为直角,求k值.
(学生板演→教师修正→学生修正)
② 讲解例6:设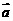 = (5, -7),
= (5, -7),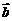 = (-6, -4),求a·b及
= (-6, -4),求a·b及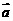 、
、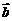 间的夹角θ(精确到1o)
间的夹角θ(精确到1o)
练习:已知A(1,0),B(3,1),C(2,0),且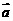 =
=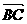 ,
,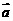 =
=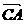 ,则
,则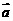 与
与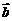 的夹角为多少?
的夹角为多少?
(学生板演→教师修正→学生修正)
1.教学坐标表示.
① 平面两向量数量积的坐标表示: 两个向量的数量积等于它们对应坐标的乘积的和.即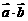
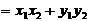
② 平面内两点间的距离公式: 如果表示向量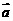 的有向线段的起点和终点的坐标分别为
的有向线段的起点和终点的坐标分别为 、
、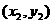 ,那么
,那么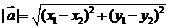
③ 向量垂直的判定: 设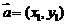 ,
, ,则
,则

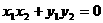
④ 两向量夹角的余弦(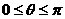 ) cosq =
) cosq =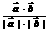
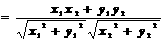
3.平面向量数量积的运算律.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com