3．在正方形ABCD中试找出有哪几对向量是平行向量.

2．若将所有单位向量的起点归结在同一起点，则其终点构成的图形是------------------.

1．判断下列式子是否正确，若不正确请指出错误原因.

①　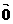 =0　　　②　.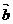-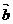=0

3．小结：向量的定义，向量由其大小与方向确定. 向量不可比较大小但其模可以比较大小.

2．教学例题：

① 例：温度有零上零下之分，“温度”是否向量？

答：不是. 因为零上零下也只是大小之分.

② 出示课本例题：84页例1. (师生共同完成：确定起点、方向、长度. 特别注意方向)

练习：在方格图中画出20N竖直向上和15N向正左方向的力.

③ 定义平行向量：方向相同或相反的两向量叫平行向量，记作：∥.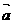

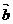规定零向量平行于任何去何从向量.

1. 教学向量的概念：

① 定义向量：既有大小又有方向的量.

练习：时间、温度、位移、质量、体积、力，哪些是向量？

②讨论：数量与向量有何区别？向量是否可以比较大小？

(数量只有大小，可以比较大小. 向量不可以比较大小)

③ 定义有向线段：带有方向的线段叫有向线段. 记作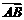，以A为起点，B为终点，几何表示时在其终点处画上箭头表示方向. (如图)

有向线段的三要素：起点、方向、长度.

④ 向量的表示：向量可以用有向线段表示，记作；也可以用字母表示，如：.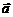

⑤ 定义模：向量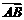的大小(长度)叫向量的模，记作，

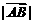⑥ 练习：画出一向正东方向以20m/s的速度行驶的小车的速度.

⑦ 定义零向量：长度为0的向量，记作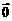，规定零向量的方向可以为任意方向.

⑧ 定义单位向量:长度为1个单位长度和向量叫单位向量.

⑨ 讨论：单位向量是否唯一？有多少个单位向量？

3. 三角函数线有没有大小和方向？是否可用有向线段表示？

2．如何定义有向线段？

1. 讨论： 到目前为止我们物理学习中学过时间、温度、位移、质量、体积、力等. 哪些是既有大小又有方向？哪些只有大小而没有方向？

7. 作业：课本P119　 练习(1)(2)