1．　 将所有共线向量移至同一起点，终点构成的图形是什么图形？

3．小结：相等到向量、共线向量.

2.教学例题：

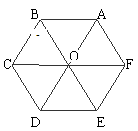
① 例1如图，设O是正六边形ABCDEF中心，分别写出图中与

向量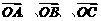相等的向量,与向量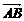平行的向量.　

(先师生共同完成，紧扣定义)

② 变式训练：

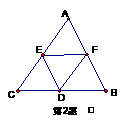变式一：与向量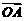长度相等的向量有多少个？(11个)

变式二：是否存在与向量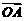长度相等、方向相反的向量？

变式三：与向量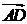共线的向量有哪些？()

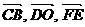1. 教学相等向量与共线向量的概念：

① 定义共线向量：任一组平行向量都可移到同一条直线上 ，所以平行向量也叫共线向量.

② 定义相等向量：长度相等且方向相同的向量叫做相等向量.

　　　 记作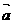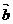：=　　　　　 规定：=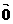

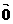
4. 试讨论：平行向量通过平移后是否可以移至同一直线上？

3. 什么是零向量、单位向量？零向量有何特点？

2．如何定义向量，怎样表示向量？(用有向线段或字母表示)

1. 有向线段的三要素是什么?

5. 作业：课本86页习题A组1、2题.

第二课时　 2.1　　 平面向量的实际背景及基本概念(二)

教学要求：掌握相等向量、共线向量的概念，会判断共线向量与相等向量.

教学重点：判断共线向量与相等向量

教学难点: 相等向量、共线向量的概念

教学过程：

4．回答下列问题：

①平行向量是否一定方向相同？

②与任何向量都平行的向量是什么向量？