
题目列表(包括答案和解析)
2、正棱柱、正棱锥、正棱台概念及面积体积;
4.求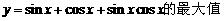
作业:课本:第151页17、18题
3.已知 ,求
,求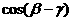 的值.
的值.
2.已知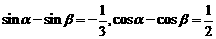 ,求
,求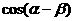 的值.
的值.
1.在△ABC中,已知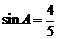 ,
, 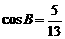 ,求
,求 的值.
的值.
2.小结:
在本小节的公式中,两角和与差的正弦、余弦公式是基础,特别是两角和的余弦公式,它几乎是这一章的中心公式,我们今后要学的其他三角公式,全部可以由它推导,甚至是诱导公式。要记住、熟练运用这些公式只有一个办法:多作题目,从做题中找感觉,感觉是从做题中得出的.
1. 教学:
⑴例题:
已知一元二次方程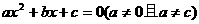 的两个根为
的两个根为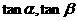 ,求
,求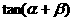 的值;
的值;
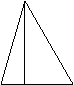 变式:求
变式:求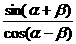 的值.说明:虽然
的值.说明:虽然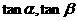 是方程的两个根,但我们并不需要求出
是方程的两个根,但我们并不需要求出
⑵求值:
(1)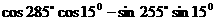 ;(2)
;(2)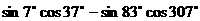
⑶求角度:
如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6,求∠BAC的度数.
⑷求三角函数最值:
已知函数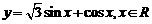 当函数
当函数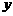 取得最大值时,求自变量
取得最大值时,求自变量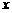 的集合.
的集合.
首先回顾两角和的正弦、余弦和正切公式,
 ;
;
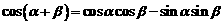 ;
;
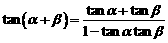 .
.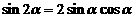 ;
;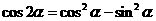 ;
;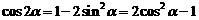 ;
; 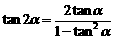
3.求证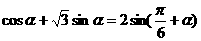 4.化简:
4.化简:
作业:课本150页11题,14题,15题
第四课时 两角和与差的正弦、余弦、正切(综合练习)
教学要求:以两角和正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式,理解推导过程,掌握其应用 教学重点:公式的理解及熟练运用、灵活运用 教学难点:公式的理解及其灵活运用 教学过程:
1. 练习:求证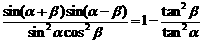 2. 变式:化简
2. 变式:化简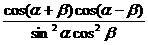
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com