6.小结：做证明题，要分析题意，明确思维起点；选择公式，把握思维方向；实施变换，运用数学思想方法

5.练习：1)求证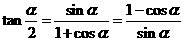

　　　 2)求证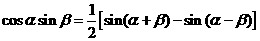(学生板演，老师讲解)

4.出示例2

　讨论：这两个式子的左右两边在结构形式上有什么不同？

(如果记，则有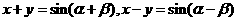。只要解上述方程组，就可以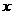求出，即求出)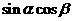

　结论：把两个三角式结构形式上的不同点作为思考的出发点，并在建立它们之间的联系进而消除不同点上下功夫，这样不仅有利于深化对和(差)角公式的理解，而且还有利于这两题内在联系的认识。

3.讨论：代数式的变换与三角变换有什么不同？

结论：代数式变换着眼于式子结构形式的变换；三角变换首先寻找式子所包含的各个角之间的联系，并以此为依据选择可以联系它们的适当公式，这是三角式恒等变换的重要特点。

2.出示例1：老师将刚才的结果进行改写，即半角公式。

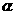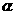1.通过讨论知道，是的二倍角，在复习的倍角公式中，让学生以代替，以代替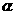

将公式进行改写。(可以请两个学生板演，老师巡查整个教室，最后师生一起检查板演的作业)

2.　　　 讨论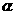：与有什么关系？(学生回答)

1.　　　 提问：前面学过的倍角公式是什么？(学生说，老师板书)

11、一个几何体按比例绘制的三视图如图所示(单位：m)

(1)　　　 画出它的直观图；(2)求几何体表面积和体积．

下图是正方体的表面展开图，在这个正方体中， BN与ED平行；②CN与BE是异面直线

①　　 CN与BM成60⁰；④DM与BN垂直．以上四个命题中，正确命题序号为　　　．

有下列棱锥：①各侧棱都相等鍀棱锥；②底面是正多边形的棱锥；③顶点在底面上射影是底面多边形外接圆圆心的棱锥；④侧面都是全等的等腰三角形的棱锥．其中为正棱锥的有

A．0个　 B．1个　 C．　 2个　　 D．3个

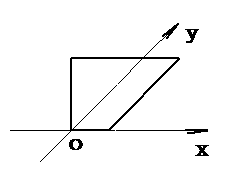
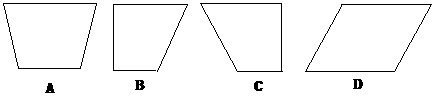
下图所示为一平面图形的直观图，则此平面图形可能是　　 (　　 )

10、一个正三棱锥，底面边长是6，侧棱长为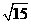，则体积为　　　　 ．