2. 练习：某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动，已知3月份达到最高价格8元，7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动，5月份销售价格最高为10元，9月份销售价最低为6元.

(1)试建立出厂价格、销售价格的模型，并求出函数解析式;

(2)假设商店每月购进这种商品m件，且当月销完，试写出该商品的月利润函数.

1. 教学三角函数应用模型：

① 出示例：某港口水深y(米)是时间t(0≤t≤24，单位：小时)的函数，记为y=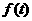，下面是某日水深数据：

经过长期观察，y=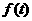的曲线可以近似看成y=Asint+b的图象.

(i)根据以上数据求出y=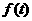的近似表达式；

(ii)船底离海底5米或者5米以上是安全的，某船的吃水深度为6.5米(船底离水面距离)，如果此船在凌晨4点进港，希望在同一天安全出港，那么此船最多在港口停留多少时间？

教法：从表中读到一些什么数据？ → 依次求各系数 → 应用模型解决问题

答案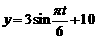：(0≤t≤24)；　 13(小时).

　　 小结：读取与分析表中的数据，是一种数学思维能力的训练. 求得模型后，把第(2)问的情景转化为一个简单的三角不等式，再运用整体思想，借助函数的图象或者单位圆可以求解.

② 练习：某海滨浴场的海浪高度y(米)是时间t(0≤t≤24，单位：小时)的函数，经过长期观察，该函数的图象可以近似地看成. 下表是测得的某日各时的浪高数据：

依规定，当浪高不低于1米时浴场才开放，试安排白天内开放浴场的具体时间段.

3. 讨论：在现实生活中，哪些现象具有周期性？(温度、白昼、振动、情绪、智力、体力等)

2. 讨论：如何由图观察得到三角函数的各系数？ 如何确定初相？(特殊点法)

1. 函数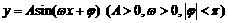最高点D的坐标是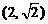，由最高点运动到相

邻的最低点时，函数图象与x轴的交点坐标是(4，0)，求此函数的表达式. (答案：)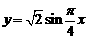

2. 作业：书P73　 习题1、2题.

第二课时：　 1.6　 三角函数模型的简单应用(二)

教学要求：掌握用待定系数法求三角函数解析式的方法；选择合理三角函数模型解决实际问题；培养学生用已有的知识解决实际问题的能力.

教学重点：待定系数法求三角函数解析式；用三角函数模型解决实际问题.

教学难点：选择合理数学模型解决实际问题.

教学过程：

1. 练习：教材P73　 练习1题.

3. 小结：给图求式；给式应用；待定系数法.

2. 练习：

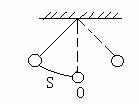
如图，单摆从某点给一个作用力后开始来回摆动，离开平衡位置O的距离s厘米和时间t秒的函数关系为.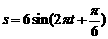

(1)单摆摆动5秒时，离开平衡位置多少厘米？

(2)单摆摆动时，从最右边到最左边的距离为多少厘米？

(3)单摆来回摆动10次所需的时间为多少秒？

1. 教学典型例题：

① 出示例1：如图，某地一天从6时到14时的温度变化曲线近似满足函数，试求这段曲线的函数解析式.

　 讨论：如何由图中的几何特征得到曲线的各参量？

　(由周期、振幅确定A、b、ω；再由特殊点确定初相ψ)

　 教师示例 → 小结：观察几何特征，转化为相应的数量关系.

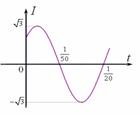② 练习：如图，它表示电流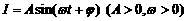在一个周期内的图象.

(i)试根据图象写出的解析式.

(ii)在任意一段秒的时间内，电流I既能取得最大值A，又能取得最小值－A吗？

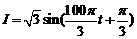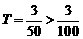　 (答案：；　 由得不可能)

② 出示例2：作出函数y＝｜sinx｜的图象，指出它的奇偶性、周期和单调区间.

　　 讨论：绝对值的几何意义？ → 作简图　 → 由图说性质

　　 变式：研究y＝｜cosx｜、y＝｜tanx｜.　 小结：数形结合思想研究函数性质.