
题目列表(包括答案和解析)
1. 求证: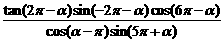 =tanα
=tanα
3. 小结:四组诱导公式的推导、记忆、运用.
2. 教学例题:
① 出示例1:求值:sin225°、 cos 、sin(-
、sin(-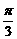 )、cos(-
)、cos(-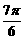 )、tan(-200°)
)、tan(-200°)
分析角的特点→学生口答. 小结:运用诱导公式的格式;注意符号.
② 出示例2:化简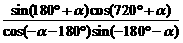
师生共练→小结:公式运用
③ 练习:已知cos(π+x)=0.5,求cos(2π-x)的值;思考:求cos(π-x)的值.
④ 讨论:四组诱导公式的作用? (分别化哪个范围的角到哪个范围?)
1. 教学诱导公式:
① 讨论:利用诱导公式(一),将任意范围内的角的三角函数值转化到0-2π后,又将如何将0-2π间的角转化到0-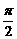 呢?
呢?
方法:设0°≤α≤90°, (写成β的分段函数)
则90°-180°间角,可写成180°-α;
180°-270°间的角,可写成180°+α;
270°-360°间的角,可写成360°-α.
② 推导π+α的诱导公式:
复习单位圆:以原点为圆心,单位长为半径的圆.
思考:角α的终边与单位圆交于点P(x, y),则sinα=?cosα=?
讨论:α与π+α终边有何关系?设交单位圆于P(x, y)、P’,则P’坐标怎样?
计算sin(π+α)、cos(π+α)、tan(π+α),并与sinα、cosα、tanα比较.
提出诱导公式二.
③ 仿上面的步骤推导-α、π-α的诱导公式.
讨论:如何由π+α、-α的诱导公式得到π-α的诱导公式? 变角:π-α=π+(-α)
列表比较四组诱导公式,观察符号情况? 口诀:函数名不变,符号看象限. (“符号”是把任意角α看成锐角时,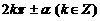 所在象限的三角函数值的符号.)
所在象限的三角函数值的符号.)
2. 提问:求任意角的三角函数值如何求?
1. 写出2kπ+α的诱导公式.
13.已知

12.已知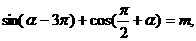
求证: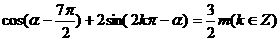
11.求下列各三角函数值:
(1)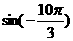 (2)
(2)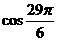 (3)
(3)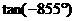
10.已知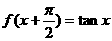 ,则
,则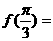 ,
,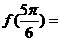
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com