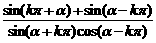3. 化简：　 (k∈Z)

2. 已知tan(π+α)＝4, 则sin(π+α)cos(π－α)＝　　　 .

1. 化简：　　 ()

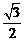3. 小结：诱导公式的记忆是重中之重；利用诱导公式，将任意角的三角函数值转化为求锐角三角函数的值，这是学习诱导公式的主要目的；注意公式之间的相互联系和变形使用公式.

2. 教学例题：

① 出示例1：求下列各角的三个三角函数的值.

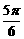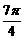、　 、　 、　 1050°、　 －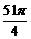

　 (示范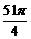－的求值；其余学生试练，四人板演；订正；小结：诱导公式的运用)

② 出示例2：求证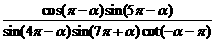＝1

　 (学生分析公式运用→试练→订正→小结：公式运用. )

③ 练习： 列表写出0-2π间所有特殊角的三个三角函数的值.

1. 教学诱导公式推导：

① 讨论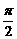：－α的终边与α的终边有何关系？ (关于直线y=x对称)

② 讨论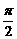：－α的诱导公式怎样？

③ 讨论：如何由前面的诱导公式得到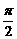+α的诱导公式？ 比较：两组诱导公式的记忆

④ 讨论：如何利用诱导公式，将任意角转化为锐角的三角函数？(转化思想)

⑤ 比较：六组诱导公式的记忆. (六组诱导公式都可统一为“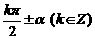”的形式，记忆的口诀为“奇变偶不变，符号看象限”. 符号看象限是把α看成锐角时原三角函数值的符号)

2. 推导2π－α的诱导公式.

1. 默写关于2kπ+α、π+α、－α、π－α的四组诱导公式

4. 作业：教材P31　 2、3、4题.

第二课时：1.3　 三角函数的诱导公式(二)

教学要求：掌握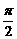α、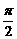+α两组诱导公式，能熟练运用六组诱导公式进行求值、化简、证明.

教学重点：熟练运用诱导公式.

教学难点：诱导公式的推导.

教学过程：

2. 化简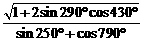：　　 (－1)