2. 讨论如何用“五点法”画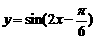的图象？(方法：取)

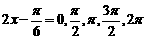1. 在同一直角坐标系中，分别作出函数 、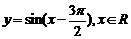的草图.

4、小结：正弦曲线、余弦曲线的几何画法、“五点法”画法及正弦、余弦函数图象的形状特征.

3. 例题讲解：

例、画出下列函数的简图：

(1)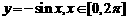；(2)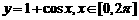. (教师引导→学生板书)

2. 教学余弦函数图象的画法：

由于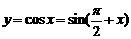，而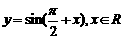的图象可以通过将正弦函数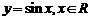的图象向左平移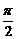个单位长度得到，因此只需将函数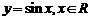的图象向左平移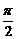个单位长度就可以得到函数的图象.

思考：如果用“五点法”作余弦函数的图象，则应抓住哪五个关键点？

1. 教学正弦函数图象的画法：

① 提问：正弦线的意义？(正弦线是与单位圆有关的平行于坐标轴的有向线段，它是正弦函数的几何表示)

② 用正弦线画出正弦函数的图象(边讲边画)：

第一步：先作单位圆，把⊙O₁十二等分(当然分得越细，图象越精确)；

第二步：十二等分后得0,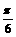, ,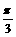,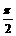…2p等角，作出相应的正弦线；

第三步：将x轴上从0到2p一段分成12等份(2p≈6.28)，若变动比例，今后图象将相应“变形”；

第四步：取点，平移正弦线，使起点与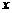轴上的点重合；

第五步：用光滑的曲线把上述正弦线的终点连接起来，得y=sinx，xÎ[0,2p]的图象；

第六步： 由终边相同的三角函数性质知y=sinx ，xÎ[2kp,2(k+1)p] kÎZ,k¹0的图象与函数y=sinx，　 xÎ[0,2p]图象相同，只是位置不同--每次向左(右)平移2p单位长.

③ 用“五点(画图)法”作正弦函数图象时，要抓住关键的五个点：(0,0)　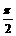 (,1)　 (p,0)　 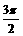(,-1)　 (2p,0). (通过学生观察正弦函数的图象，找出体现图象形状特征的点，再来讲“五点法”.)

“五点法”的优点是方便，但精确度不高，熟练后才使用.

2. 提问：如何作出正弦函数的图象？(利用正弦线可以画出较精确的正弦函数图象)

1. 讨论：实数集与角的集合之间可以建立一一对应关系，而一个确定的角又对应着唯一确定的正弦(余弦)值. 由这个对应法则所确定的函数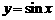(或)叫做正弦函数(或余弦函数)，其定义域是.

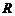5. 作业：教材P31　 5、6、7题.

4. 求函数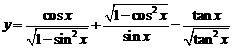的值域.