1. 练习：求出下列函数的最小正周期，并说明下列函数是否有最大值、最小值，如果有，请写出取最大值、最小值时的自变量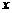的集合.

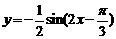(1)；(2).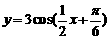

2.作业：教材P52　第2题

第三课时　 　1.4.3　 　正弦函数、余弦函数的性质(二)

教学要求：掌握正弦函数、余弦函数的单调性，并会运用单调性，比较三角函数值的大小，求三角型函数的单调区间.

教学重点：正弦函数、余弦函数的单调性.

教学难点：正弦函数、余弦函数单调性的应用.

教学过程：

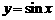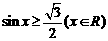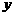1.作出函数的图象，1)解不等式：；2)求时的值域.

4、小结：正弦、余弦函数的周期性、奇偶性、最大值、最小值，数形结合思想.

3. 教学正弦函数、余弦函数的最大值、最小值：

观察图象发现，正弦曲线、余弦曲线均有最高点和最低点，即函数值都有最大值、最小值.

例2：下列函数有最大值、最小值吗？如果有，请写出取最大值、最小值时的自变量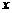的集合，并说出最大值、最小值分别是什么？

(1)；(2).

(教师引导→学生分析→教师总结并板书)

练习：教材P45　第3题

2. 教学正弦函数、余弦函数的奇偶性：

由图象观察，结合诱导公式知，正弦函数是奇函数，余弦函数是偶函数.

1. 教学正弦、余弦函数的周期性：

① 正弦函数值具有“周而复始”的变化规律，这一点可以从正弦线的变化规律中看出，还可以从诱导公式中得到反映，即当自变量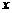的值增加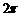的整数倍时，函数值重复出现.

②周期函数的定义：对于函数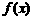，如果存在一个非零常数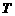，使得当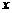取定义域内的每一个值时，都有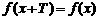，那么函数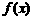就叫做周期函数，非零常数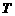叫做这个函数的周期.

(周期函数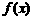的周期不唯一，都是它的周期，所有周期中最小的正数就叫做它的最小正周期)

③正弦函数、余弦函数都是周期函数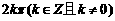，都是它们的周期，最小正周期是.

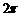例1：求下列函数的周期：

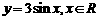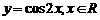(1)；(2)；(3).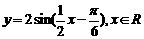

(师生共析→教师板书→学生观察→总结规律：这些函数的周期与解析式中哪些量有关？)

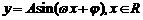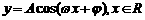④结论：形如(或)的函数的最小正周期.

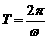2. 讨论：由正弦、余弦函数的图象有哪些特征？

1. 提问：①函数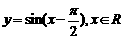的图象与函数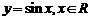的图象有什么关系？(学生经思考后回答)②如何作出函数的图象？(学生板书→教师总结方法)

3. 作业：教材P52　第1题

第二课时　 1.4.2　 　正弦函数、余弦函数的性质(一)

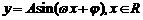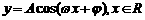教学要求：掌握正弦函数、余弦函数的周期性、奇偶性和最大值、最小值，会求形如(或)的函数的最小正周期，并会利用正弦、余弦函数的最大值、最小值求相关函数的值域.

教学重点：正弦函数、余弦函数的性质(包括周期性、奇偶性和最大值、最小值).

教学难点：正弦函数、余弦函数性质的应用.

教学过程：