1. 教学正切函数的性质：

① 定义域：；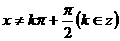

② 周期性：由诱导公式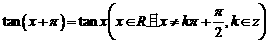可知，正切函数是周期函数，最小正周期是.

③ 奇偶性：由诱导公式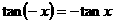可知，正切函数是奇函数.

④ 单调性：由正切线的变化规律可以看出，正切函数在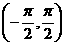内是增函数，又由正切函数的周期性可知，正切函数在开区间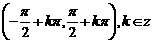内都是增函数.

⑤ 值域：正切函数的值域是实数集R.

2. 提问：能否依照研究正弦、余弦函数性质的方法来研究正切函数的性质和图象？

1. 复习：正弦、余弦函数的图象和性质；研究正弦、余弦函数性质的方法？ 　

3. 作业：教材P52　第5题

第四课时　 1.4.4　 正切函数的性质和图象

教学要求：掌握正切函数的性质，学会画正切函数的图象，深化研究函数性质的思想方法.

教学重点：正切函数的性质和图象.

教学难点：正切函数性质的应用.　

教学过程：

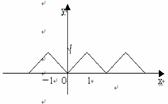
2. 已知函数的图象如图所示，试回答下列问题：

(1)求函数的周期性；(2)画出函数的图象；

(3)你能写出函数的解析式吗？

1. 练习：教材P52　第1(2)题

3. 小结：正弦、余弦函数的单调性；整体代入法求单调区间.

2. 教学正弦、余弦函数的应用：

例1：利用三角函数的单调性，比较下列各组数的大小：

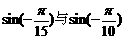(1)与；(2)；(3).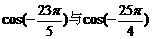

(学生口答第1小题→学生板书第2小题→师生共析第3小题→教师板书第3小题)

练习：教材P45　第5题

例2：求函数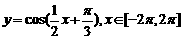的递增区间.

(师生共析→教师板书→小结：整体代入，解不等式→变式：解不等式)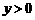

练习：①求出上例中函数的单调递减区间. ②教材P45　第6题

例3：求函数的递增区间.

(师生共析→学生板书)

1. 教学正弦、余弦函数的单调性：

　先在正弦函数的一个周期的区间上(如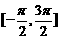)讨论它的单调性，再利用它的周期性，将单调性扩展到整个定义域.

观察图象可得，①正弦函数在每一个闭区间(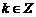)上都是增函数，其值从－1增大到1；在每一个闭区间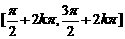(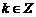)上都是减函数，其值从1减到－1.②余弦函数在每一个闭区间(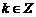)上都是增函数，其值从－1增大到1；在每一个闭区间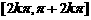(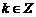)上都是减函数，其值从1减到－1.

2. 提问：如何比较与的大小？