

题目列表(包括答案和解析)
1.周期函数定义
定义 对于函数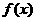 ,如果存在一个不为零的常数
,如果存在一个不为零的常数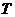 ,使得当
,使得当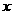 取定义域内的每一个值时,
取定义域内的每一个值时, 都成立,那么就把函数
都成立,那么就把函数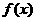 叫做周期函数,不为零的常数
叫做周期函数,不为零的常数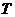 叫做这个函数的周期.
叫做这个函数的周期.
请你判断下列函数的周期
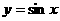



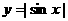 y=tan x
y=tan |x| y=|tan x|
y=tan x
y=tan |x| y=|tan x| 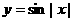
例 求函数f(x)=3sin 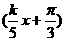 (
( 的周期。并求最小的正整数k,使他的周期不大于1
的周期。并求最小的正整数k,使他的周期不大于1

注意 理解函数周期这个概念,要注意不是所有的周期函数都有最小正周期,如常函数f(x)=c(c为常数)是周期函数,其周期是异于零的实数,但没有最小正周期.
结论:如函数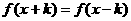 对于
对于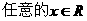 ,那么函数f(x)的周期T=2k;
如函数
,那么函数f(x)的周期T=2k;
如函数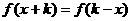 对于
对于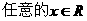 ,那么函数f(x)的对称轴是
,那么函数f(x)的对称轴是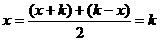
(1)同角三角函数的关系
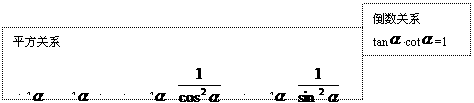

作用:已知某角的一个三角函数值,求它的其余各三角函数值。
(2)诱导公式:
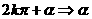 :
,
,
;
:
,
,
;
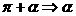 :
,
,
;
:
,
,
;
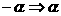 : ,
,
;
: ,
,
;
 :
,
,
;
:
,
,
;
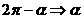 :
,
,
;
:
,
,
;
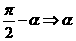 :
,
,
;
:
,
,
;
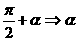 :
,
,
;
:
,
,
;
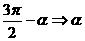 :
,
,
;
:
,
,
;
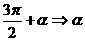 :
,
,
;
:
,
,
;
诱导公式可用概括为:
 2K
2K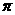 ±
±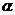 ,-
,-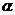 ,
,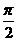 ±
±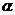 ,
,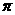 ±
±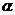 ,
,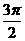 ±
±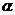 的三角函数 奇变偶不变,符号看象限
的三角函数 奇变偶不变,符号看象限  的三角函数
的三角函数
作用:“去负--脱周--化锐”,是对三角函数式进行角变换的基本思路.即利用三角函数的奇偶性将负角的三角函数变为正角的三角函数--去负;利用三角函数的周期性将任意角的三角函数化为角度在区间[0o,360o)或[0o,180o)内的三角函数--脱周;利用诱导公式将上述三角函数化为锐角三角函数--化锐.
(3)同角三角函数的关系与诱导公式的运用:
①已知某角的一个三角函数值,求它的其余各三角函数值。
注意:用平方关系,有两个结果,一般可通过已知角所在的象限加以取舍,或分象限加以讨论。
②求任意角的三角函数值。
步骤:
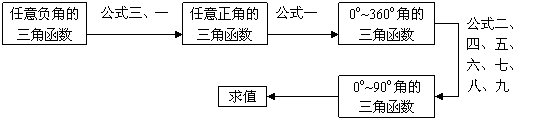

③已知三角函数值求角:注意:所得的解不是唯一的,而是有无数多个.
步骤: ①确定角 所在的象限;
所在的象限;
②如函数值为正,先求出对应的锐角 ;如函数值为负,先求出与其绝对值对
;如函数值为负,先求出与其绝对值对
应的锐角 ;
;
③根据角 所在的象限,得出
所在的象限,得出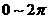 间的角--如果适合已知条件的角在第二限;则它是
间的角--如果适合已知条件的角在第二限;则它是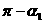 ;如果在第三或第四象限,则它是
;如果在第三或第四象限,则它是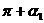 或
或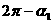 ;
;
④如果要求适合条件的所有角,再利用终边相同的角的表达式写出适合条件的所有角的集合。
如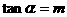 ,则
,则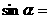 ,
, ;
;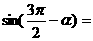 ;
; _________。
_________。
注意:巧用勾股数求三角函数值可提高解题速度:(3,4,5);(6,8,10);(5,12,13);(8,15,17);
(1)任意角的三角函数定义:
以角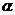 的顶点为坐标原点,始边为
的顶点为坐标原点,始边为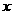 轴正半轴建立直角坐标系,在角
轴正半轴建立直角坐标系,在角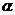 的终边上任取一个异于原点的点
的终边上任取一个异于原点的点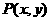 ,点
,点 到原点的距离记为
到原点的距离记为 ,则
,则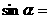 ;
; ;
; ;
;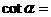 ;
; ;
; ;
;
如:角 的终边上一点
的终边上一点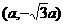 ,则
,则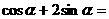 。注意r>0
。注意r>0
(2)在图中画出角 的正弦线、余弦线、正切线;
的正弦线、余弦线、正切线;
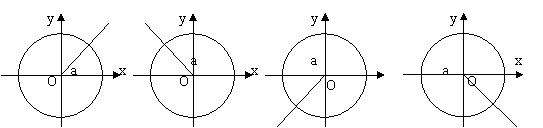

比较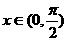 ,
,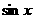 ,
, ,
,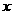 的大小关系:
。
的大小关系:
。
(3)特殊角的三角函数值:
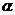 |
0 |
 |
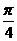 |
 |
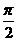 |
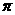 |
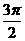 |
sin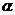 |
|
|
|
|
|
|
|
cos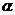 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
②写出图中所表示的区间角:
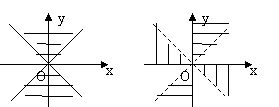
(4)正确理解角:
要正确理解“ 间的角”=
;
间的角”=
;
“第一象限的角”= ;“锐角”= ;
“小于 的角”=
;
的角”=
;
(5)由 的终边所在的象限,通过
来判断
的终边所在的象限,通过
来判断 所在的象限。
所在的象限。
来判断 所在的象限
所在的象限
(6)弧度制:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零;任一
已知角 的弧度数的绝对值
的弧度数的绝对值 ,其中
,其中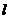 为以角
为以角 作为圆心角时所对圆弧的长,
作为圆心角时所对圆弧的长, 为圆的半径。注意钟表指针所转过的角是负角。
为圆的半径。注意钟表指针所转过的角是负角。
(7)弧长公式: ;半径公式: ;
扇形面积公式: ;
(1)在直角坐标系内讨论角:
角的顶点在原点,始边在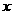 轴的正半轴上,角的终边在第几象限,就说过角是第几象限的角。若角的终边在坐标轴上,就说这个角不属于任何象限,它叫象限界角。
轴的正半轴上,角的终边在第几象限,就说过角是第几象限的角。若角的终边在坐标轴上,就说这个角不属于任何象限,它叫象限界角。
(2)①与 角终边相同的角的集合:
角终边相同的角的集合:
与 角终边在同一条直线上的角的集合: ;
角终边在同一条直线上的角的集合: ;
与 角终边关于
角终边关于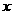 轴对称的角的集合:
;
轴对称的角的集合:
;
与 角终边关于
角终边关于 轴对称的角的集合:
;
轴对称的角的集合:
;
与 角终边关于
角终边关于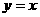 轴对称的角的集合:
;
轴对称的角的集合:
;
②一些特殊角集合的表示:
终边在坐标轴上角的集合: ;
终边在一、三象限的平分线上角的集合: ;
终边在二、四象限的平分线上角的集合: ;
终边在四个象限的平分线上角的集合: ;
(3)区间角的表示:
①象限角:第一象限角: ;第三象限角: ;
13.已知函数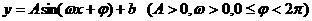 在同一周期内有最高点
在同一周期内有最高点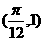 和最低点
和最低点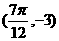 ,求此函数的解析式
,求此函数的解析式
12.已知函数y=3sin3x.
(1)作出函数在x∈[,]上的图象.
(2)求(1)中函数的图象与直线y=3所围成的封闭图形的面积
(3)求f(x)的最小正周期;
(4)求f(x)的单调区间;
(5)求f(x)图象的对称轴,对称中心.(20分)
11.函数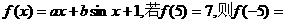
10.函数y=sin(-2x)的单调递增区间是__________
9.下列函数中,周期为π,且在(0, )上单调递增的是
A.y=tan|x| B.y=|cotx| C.y=|sinx| D.y=|cosx|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com