
题目列表(包括答案和解析)
1. 写出终边在第一象限的角的集合?第二象限呢?第三象限呢?第四象限呢?直线y=-x呢?
3. 小结:角的推广;象限角的定义;终边相同角的表示;终边落在坐标轴时等;区间角表示.
2.教学例题:
① 出示例1:在0°-360°间,找出下列终边相同角:-150°、1040°、-940°.
(讨论计算方法:除以360求正余数 →试练→订正)
② 出示例2:写出与下列终边相同的角的集合,并写出-720°-360°间角.
120°、-270°、1020°
(讨论计算方法:直接写,分析k的取值 →试练→订正)
③ 讨论:上面如何求k的值? (解不等式法)
④ 练习:写出终边在x轴上的角的集合,y轴上呢?坐标轴上呢?第一象限呢?
⑤ 出示例3:写出终边直线在y=x上的角的集合S, 并把S中适合不等式
的元素 写出来. (师生共练→小结)
写出来. (师生共练→小结)
1.教学角的概念:
① 定义正角、负角、零角:按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,未作任何旋转所形成的角叫零角.
② 讨论:推广后角的大小情况怎样? (包括任意大小的正角、负角和零角)
③ 示意几个旋转例子,写出角的度数.
④ 如何将角放入坐标系中?→定义第几象限的角.
(概念:角的顶点与原点重合,角的始边与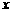 轴的非负半轴重合. 那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角. )
轴的非负半轴重合. 那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角. )
⑤ 练习:试在坐标系中表示300°、390°、-330°角,并判别在第几象限?
⑥ 讨论:角的终边在坐标轴上,属于哪一个象限?
结论:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角.
口答:锐角是第几象限角?第一象限角一定是锐角吗?再分别就直角、钝角来回答这两个问题.
⑦ 讨论:与60°终边相同的角有哪些?都可以用什么代数式表示?
与α终边相同的角如何表示?
⑧ 结论:与α角终边相同的角,都可用式子k×360°+α表示,k∈Z,写成集合呢?
⑨ 讨论:给定顶点、终边、始边的角有多少个?
注意:终边相同的角不一定相等;但相等的角,终边一定相同;终边相同的角有无数多个,它们相差360°的整数倍
2.讨论:实际生活中是否有些角度超出初中所学的范围? → 说明研究推广角概念的必要性
(钟表;体操,如转体720°;自行车车轮;螺丝扳手)
1.提问:初中所学的角是如何定义?角的范围?
(角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形;0°-360°)
三角变换是运算化简的过程中运用较多的变换,提高三角变换能力,要学会创设条件,灵活运用三角公式,掌握运算,化简的方法和技能.常用的数学思想方法技巧如下:
(1)角的变换:在三角化简,求值,证明中,表达式中往往出现较多的相异角,可根据角与角之间的和差,倍半,互补,互余的关系,运用角的变换,沟通条件与结论中角的差异,使问题获解,对角的变形如:
①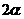 是
是 的二倍;
的二倍;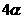 是
是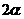 的二倍;
的二倍; 是
是 的二倍;
的二倍; 是
是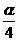 的二倍;
的二倍;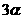 是
是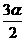 的二倍;
的二倍; 是
是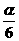 的二倍;
的二倍; 是
是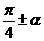 的二倍。
的二倍。
②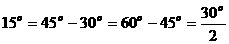 ;问:
;问: ;
;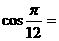 ;
;
③ ;④
;④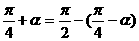 ;
;
⑤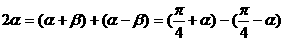 ;等等
;等等
(2)函数名称变换:三角变形中,常常需要变函数名称为同名函数。如在三角函数中正余弦是基础,通常化切、割为弦,变异名为同名。
(3)常数代换:在三角函数运算,求值,证明中,有时需要将常数转化为三角函数值,例如常数“1”的代换变形有:
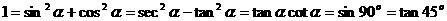
(4)幂的变换:降幂是三角变换时常用方法,对次数较高的三角函数式,一般采用降幂处理的方法。常用降幂公式有:
;
。降幂并非绝对,有时需要升幂,如对无理式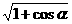 常用升幂化为有理式,常用升幂公式有:
;
;
常用升幂化为有理式,常用升幂公式有:
;
;
(5)公式变形:三角公式是变换的依据,应熟练掌握三角公式的顺用,逆用及变形应用。
如: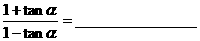 ;
; 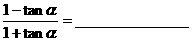 ;
;
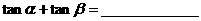 ;
; ;
;
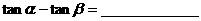 ;
; ;
;
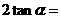 ;
;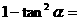 ;
;
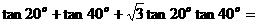 ;
;
 =
;
=
;
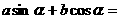 =
;
=
;
(其中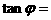 ;)
;)
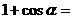 ;
;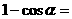 ;
;
(6)三角函数式的化简运算通常从:“角、名、形、幂”四方面入手;
基本规则是:切割化弦,异角化同角,复角化单角,异名化同名,高次化低次,无理化有理,和积互化,特殊值与特殊角的三角函数互化。
如: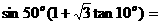 ;
;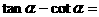 ;
;
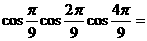 ;
;
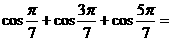 ;推广:
;推广:
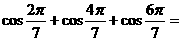 ;推广:
;推广:

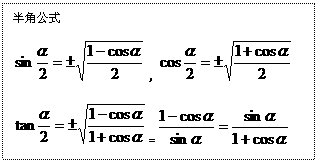

三倍角公式: ;
;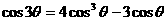 ;
;
3、图像的平移
对函数y=Asin(ωx+j)+k (A>0, ω>0, j≠0, k≠0),其图象的基本变换有:
(1)振幅变换(纵向伸缩变换):是由A的变化引起的.A>1,伸长;A<1,缩短.
(2)周期变换(横向伸缩变换):是由ω的变化引起的.ω>1,缩短;ω<1,伸长.
(3)相位变换(横向平移变换):是由φ的变化引起的.j>0,左移;j<0,右移.
(4)上下平移(纵向平移变换): 是由k的变化引起的.k>0, 上移;k<0,下移
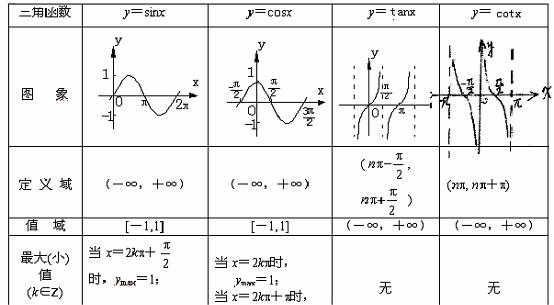
2.图像

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com