2. 一扇形的中心角是54°，它的半径为20cm，求扇形的周长和面积.

1. 时间经过2小时30分，时针和分针各转了多少弧度？

3. 小结：

扇形弧长公式、面积公式；弧度制的运用；计算器使用.

2. 练习：

①. 用弧度制写出与下列终边相同的角，并求0-2π间的角.

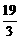π、－675°

② 用弧度制表示终边在x轴上角的集合、终边在y轴上角的集合？终边在第三象限角的集合？

③ 讨论：α＝k×360°+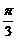与β＝2kπ+30°是否正确？

④ α与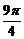－的终边相同，且－2π<α<2π，则α＝　　　 .

⑤ 已知扇形AOB的周长是6cm，该扇形的中心角是1弧度，求该扇形的面积.

解法：设扇形的半径为r，弧长为l，列方程组而求.

1. 教学例题：

① 出示例：用弧度制推导：S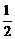＝LR；.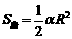

分析：先求1弧度扇形的面积(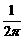πR)→再求弧长为L、半径为R的扇形面积？

方法二：根据扇形弧长公式、面积公式，结合换算公式转换.

② 练习：扇形半径为45，圆心角为120°，用弧度制求弧长、面积.

③ 出示例：计算sin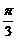、tan1.5、cos

(口答方法→共练→小结：换算为角度；计算器求)

② 练习：求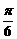、、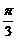的正弦、余弦、正切.

3. 口答下列特殊角的弧度数：0°、30°、45°、60°、90°、120°、135°、…

2. 弧度与角度互换：－π、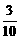π、－210°、75°

1. 提问：什么叫1弧度的角？1度等于多少弧度？1弧度等于多少度？扇形弧长公式？

3. 作业：教材P11　 5、7、8题.

第三课时：1.1.2　 弧度制(二)

教学要求：更进一步理解弧度的意义，能熟练地进行弧度与角度的换算. 掌握弧长公式，能用弧度表示终边相同的角、象限角和终边在坐标轴上的角. 掌握并运用弧度制表示的弧长公式、扇形面积公式

教学重点：掌握扇形弧长公式、面积公式.

教学难点：理解弧度制表示.

教学过程：

2. 用弧度制表示下列角的集合：终边在直线y=x； 终边在第二象限； 终边在第一象限.