
题目列表(包括答案和解析)
2.设p = (2,7),q = (x,-3),求x的取值范围使得:
①p与q的夹角为钝角 ②p与q的夹角为锐角。
解:①p与q的夹角为钝角Û p•q<0Û2x-21<0Û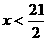 即xÎ(-∞,
即xÎ(-∞,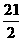 )
)
 ②p与q的夹角为锐角Û p•q>0Û2x-21>0Û
②p与q的夹角为锐角Û p•q>0Û2x-21>0Û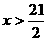 即xÎ(
即xÎ(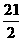 ,+∞)
,+∞)
1.已知|a| = 3,b = (1,2),且a∥b,求a的坐标。
解:设a = (x,y) ∵|a| = 3 ∴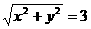 …①
…①
又:∵a∥b ∴1•y - 2•x = 0 …②
解之: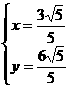 或
或
即:a = (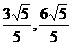 ) 或a = (
) 或a = (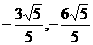 )
)
3.
2. 关于距离公式
关于距离公式
1.数量积的坐标表示:a•b = x1x2 + y1y2
7.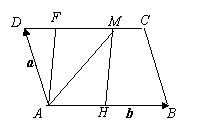
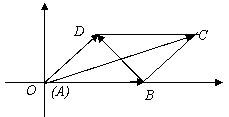
 如图:已知在 ABCD中,AH=HD,BF=MC=
如图:已知在 ABCD中,AH=HD,BF=MC=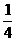 BC,设
BC,设 =a,
=a,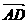 =b,试用a、b分别表示
=b,试用a、b分别表示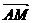 、
、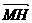 、
、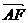 。
。
 解:∵ ABCD中,BF=MC=
解:∵ ABCD中,BF=MC= BC,
BC,
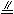 ∴FM=
∴FM= BC=
BC= AD=AH ∴FM AH
AD=AH ∴FM AH
∴四边形AHMF也是平行四边形,∴AF=HM
又: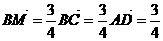 a ,
而
a ,
而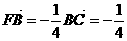 b
b
∴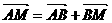 = a +
= a +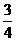 b ,
b ,
 = -
= -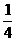 b - a
b - a
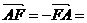 -(-
-(-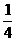 b - a) =
b - a) = 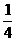 b + a
b + a
6.设非零向量a、b不共线,c=ka+b,d=a+kb (kÎR),若c∥d,试求k。
解:∵c∥d ∴由向量共线的充要条件得:c =λd (λÎR)
即:ka+b=λ(a+kb) ∴(k-λ)a + (1-λk)b = 0
又∵a、b不共线 ∴由平面向量的基本定理: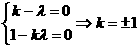
5.设x为未知向量,a、b为已知向量,解方程2x-(5a+3x-4b)+ a-3b=0
a-3b=0
解:原方程可化为:(2x - 3x)
+ (-5a + a) + (4b-3b)
= 0 ∴x =
a) + (4b-3b)
= 0 ∴x =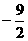 a + b
a + b
4.如图:1°已知a、b、c、d,求作向量a-b、c-d。
 2°已知a、b、c,求作a + c - b
2°已知a、b、c,求作a + c - b
3.a =“向东走5km”,b =“向西走12km”,试求a+b的长度与方向。
解:如图: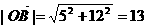 (km)
(km)
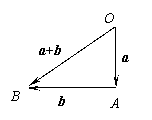 tanÐAOB =
tanÐAOB =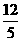 , ∴ÐAOB = arctan
, ∴ÐAOB = arctan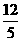
∴a + b的长为13km,方向与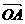 成arctan
成arctan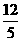 的角。
的角。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com