
题目列表(包括答案和解析)
4.运算律
3.性质1° -5°
2.a•b>0Û0≤q<90°;a•b=0Û=q=90° 即a^b;a•b<0Û90°<q≤180°
1.定义、其结果是一个数量。
8.已知函数 y = -2(x - 2)2 -1的图象经过按a平移后使得抛物线顶点在y轴上,且在x轴上截得的弦长为4,求平移后函数解析式和a。
解:依题意:平移后的函数解析式为:y = 2x2 + n
平移前顶点为(2,-1),平移后顶点为(0,n),
∴a = (0-2,n-(-1)) = (-2,n+1)
在y = 2x2 + n中, 令y = 0,x =±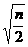 ;
;
∵函数在x轴上截得的弦长为4 ∴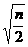 = 2,∴n = 8,
= 2,∴n = 8,
∴平移后的解析式为:y = 2x2 + 8,且a = (-2,9)。
7.将函数 y = 2x2 的图象经过怎样的平移可得到 y = 2x2 - 4x + 3的图象?
解:y = 2x2 - 4x + 3 = 2(x - 1)2 +1
即向右平移1个单位,再向上平移1个单位,
即按a = (1,1)的方向平移即得的图象。
6.将点A(-3,2)平移到点P(2,-4),按此方式,若点B平移后的坐标为(-5,1),试求点B的坐标。
解:依题意:平移向量a = 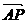 = (5,-6),
= (5,-6),
设B的坐标为(x,y),由平移公式: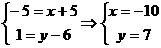
即点B坐标为(-10,7)
5.求证:cos(a-b) = cosacosb + sinasinb
证:设a、b终边上以原点为起点的向量分别为a、b,夹角为q,
则 a-b = 2kp±q (kÎZ)
∵a = (|a|cosa, |a|sina) b = (|b|cosb, |b|sinb)
∴a•b = |a|cosa•|b|cosb + |a|sina•|b|sinb =|a||b|(cosacosb + sinasinb)
又:∴a•b = |a||b|cosq = |a||b|cos[2kp±(a-b)] = |a||b|cos (a-b)
∴|a||b|(cosacosb + sinasinb) = |a||b|cos (a-b)
∵a ¹ 0 , b ¹ 0 ∴cos(a-b) = cosacosb + sinasinb
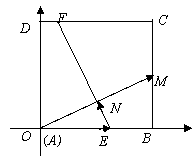
4.如图:ABCD是正方形,M是BC的中点,
将正方形折起使点A与M重合,设折痕为EF,
若正方形面积为64,求△AEM的面积。
解:如图,建立直角坐标系,
显然EF是AM的中垂线,
∴N是AM的中点,又正方形边长为8 ∴M(8,4), N(4,2)
设点E(e,0),则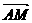 =(8,4),
=(8,4),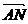 =(4,2),
=(4,2),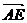 =(e,0),
=(e,0),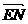 =(4-e,2),
=(4-e,2),
由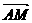 ^
^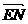 得:
得: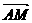 •
•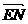 = 0 即:(8,4)•(4-e,2) = 0
= 0 即:(8,4)•(4-e,2) = 0
解之:e = 5 即|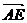 | = 5 ∴S△AEM =
| = 5 ∴S△AEM = |
|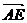 ||
||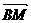 | =
| = ×5×4 = 10
×5×4 = 10
3.求证:菱形的对角线互相垂直。
证:设B(b1,0),D(d1,d2),
则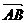 = (b1,0),
= (b1,0), 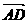 = (d1,d2)
= (d1,d2)
于是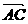 =
=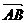 +
+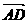 = (b1,0) + (d1,d2) = (b1+d1,d2)
= (b1,0) + (d1,d2) = (b1+d1,d2)
 =
=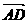 -
-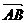 = (d1 -b1,d2)
= (d1 -b1,d2)
∵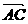 •
• = (b1+d1)(d1
-b1) + d2d2 = (d12
+ d22)- b12
= (b1+d1)(d1
-b1) + d2d2 = (d12
+ d22)- b12
 = |
= |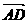 |2 - b12
= |
|2 - b12
= |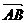 |2 - b12
= b12
- b12
= 01
|2 - b12
= b12
- b12
= 01
∴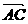 ^
^
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com