
题目列表(包括答案和解析)
3.在△ABC中,若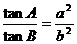 ,判断△ABC的形状。
,判断△ABC的形状。
解一:由正弦定理: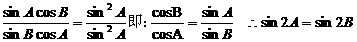
∴2A = 2B 或 2A = 180° - 2B 即:A= B 或 A + B = 90°
∴△ABC为等腰或直角三角形
解二: 由题设: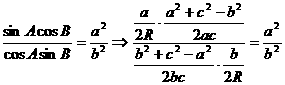
化简:b2(a2 + c2 - b2) = a2(b2 + c2 - a2) ∴(a2 -b2)(a2 + b2 - c2)=0
 ∴a = b或 a2 + b2 = c2 ∴△ABC为等腰或直角三角形
∴a = b或 a2 + b2 = c2 ∴△ABC为等腰或直角三角形
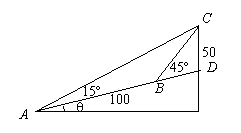
2.已知:在△ABC中,ÐA=45°,AB=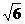 ,BC=2,解此三角形。
,BC=2,解此三角形。
解一: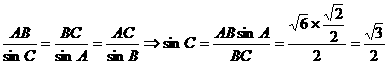
∴当ÐC = 60°时, ÐB = 75° ∴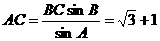
∴当ÐC = 120°时, ÐB = 15° ∴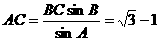
解二:设AC = b,由余弦定理: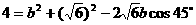
即: 解得:
解得: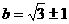
再由余弦定理: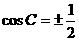 ∴ÐC = 60°或120°, ÐB = 75°或15°
∴ÐC = 60°或120°, ÐB = 75°或15°
1.证明射影定理:a = bcosC + ccosB;b = acosC + ccosA;c = acosB + bcosA
证一:右边 =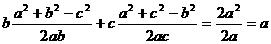 = 左边
= 左边
证二:右边 = 2RsinBcosC + 2RsinCcosB=2Rsin(B+C)=2RsinA= a = 左边
其余两式同
7.如图,AD、BE、CF是△ABC的三条高,
求证:AD、BE、CF相交于一点。
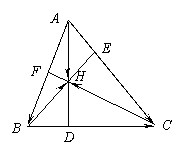 证:设BE、CF交于一点H,
证:设BE、CF交于一点H,
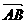 = a,
= a,  = b,
= b, 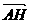 = h,
= h,
则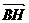 = h - a
,
= h - a
, 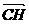 = h - b
,
= h - b
, 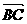 = b - a
= b - a
∵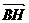 ^
^ ,
, 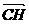 ^
^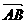
∴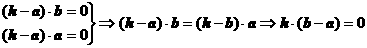
∴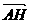 ^
^
又∵点D在AH的延长线上,∴AD、BE、CF相交于一点
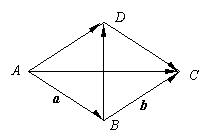
6.用向量方法证明:菱形对角线互相垂直。
证:设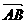 =
= = a ,
= a , 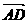 =
=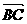 = b
= b
∵ABCD为菱形 ∴|a| = |b|
∴ ×
×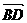 = (b + a)(b - a) = b2 - a2 = |b|2
- |a|2
= 0
= (b + a)(b - a) = b2 - a2 = |b|2
- |a|2
= 0
∴ ^
^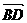
5.已知a、b都是非零向量,且a + 3b与7a - 5b垂直,
a - 4b与7a - 2b垂直,求a与b的夹角。
解:由(a + 3b)(7a - 5b) = 0 Þ 7a2 + 16a×b -15b2 = 0 ①
(a - 4b)(7a - 2b) = 0 Þ 7a2 - 30a×b + 8b2 = 0 ②
两式相减:2a×b = b2
代入①或②得:a2 = b2
 设a、b的夹角为q,则cosq =
设a、b的夹角为q,则cosq =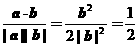
∴q = 60°
4.已知非零向量a、b,满足a ¹±b,
求证:b-a垂直于a+b的充要条件是|a| = |b|
证:由题设:b-a与a+b均为非零向量
必要性:设b-a垂直于a+b,则(b-a)(a+b) = 0
又:(b-a)(a+b) = b2 - a2 = |b|2 - |a|2
∴|b|2 - |a|2 = 0 即:|a| = |b|
充分性:设|a| = |b|,则(b-a)(a+b) = b2 - a2 = |b|2 - |a|2 = 0
即:(b-a)(a+b) = 0 ∴(b-a) ^ (a+b)
3.设非零向量a、b、c、d,满足d = (a•c) b - (a•b)c,求证:a^d
证:内积a•c与a•b均为实数,
∴a•d = a•[(a•c) b - (a•b)c] = a•[(a•c) b] - a•[(a•b)c]
= (a•b)(a•c) - (a•c)(a•b) = 0
∴a^d
2.求证:|a + b |≤|a| + |b|
证:|a + b |2 = (a + b)2 = |a|2 + |b|2 + 2a•b = |a|2 + |b|2 + 2|a||b|cosq
≤ |a|2 + |b|2 + 2|a||b| = ( |a| + |b| )2
即:|a + b |≤|a| + |b|
1.已知|a| = 5,|b| = 8,a 与b的夹角为60°,求 |a + b |
解:a•b = |a||b|cos60° = 5×8× = 20
= 20
∴|a + b |2 = (a + b)2 = |a|2 + |b|2 + 2a•b = 129
∴|a
+ b
| =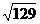
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com