
题目列表(包括答案和解析)
6.某人骑车以每小时a公里的速度向东行驶,感到风从正东方向吹来,而当速度为2a时,感到风从东北方向吹来,试求实际风速和方向。
 解:设a表示此人以每小时a公里的速度向东行驶的向量,
解:设a表示此人以每小时a公里的速度向东行驶的向量,
无风时此人感到风速为-a,
设实际风速为v,
那么此时人感到的风速为v - a,
设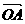 = -a,
= -a,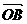 = -2a
= -2a
∵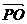 +
+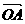 =
=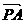 ∴
∴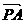 = v - a,这就是感到由正北方向吹来的风速,
= v - a,这就是感到由正北方向吹来的风速,
∵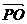 +
+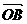 =
=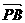 ∴
∴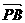 = v -2a,于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是
= v -2a,于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是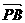 ,
,
由题意:ÐPBO = 45°, PA^BO, BA = AO
从而,△POB为等腰直角三角形,∴PO = PB =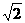 a 即:|v
| =
a 即:|v
| =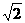 a
a
∴实际风速是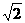 a的西北风
a的西北风
5.已知:平面上三点O、A、B不共线,求证:平面上任一点C与A、B共线的充要条件是存在实数λ和μ,使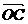 =λ
=λ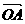 + μ
+ μ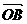 ,且λ+ μ = 1。
,且λ+ μ = 1。
证:必要性:设A,B,C三点共线,则可设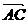 = t
= t (tÎR)
(tÎR)
则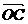 =
=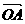 +
+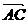 =
=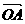 + t
+ t =
=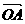 + t(
+ t(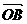 -
-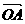 ) = (1-t)
) = (1-t)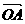 + t
+ t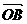
令1-t =λ,t = μ,则有: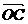 =λ
=λ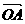 + μ
+ μ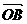 ,且λ+ μ = 1
,且λ+ μ = 1
充分性: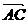 =
=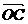 -
-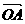 =λ
=λ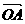 + μ
+ μ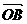 -
-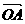 = (λ-1)
= (λ-1)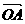 + μ
+ μ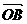
= -μ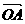 + μ
+ μ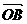 = μ(
= μ(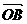 -
-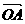 ) = μ
) = μ
∴三点A、B、C共线
4.求证:起点相同的三个非零向量a、b、3a -2b的终点在同一直线上。
证:依题意,可设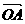 = a,
= a, 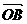 = b,
= b, 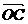 = 3a -2b
= 3a -2b
 =
=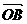 -
-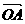 = b - a
,
= b - a
, 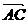 =
=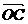 -
-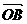 = 3a -2b - a = 2(a
- b)
= 3a -2b - a = 2(a
- b)
∴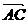 = -2
= -2 由于
由于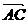 ,
, 起点均为A,∴三点A,B,C共线,
起点均为A,∴三点A,B,C共线,
即起点相同的三个非零向量a、b、3a -2b的终点在同一直线上
3.设 =
=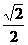 (a+5b),
(a+5b),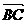 =-2a
+ 8b,
=-2a
+ 8b,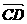 =3(a -b),求证:A,B,D三点共线。
=3(a -b),求证:A,B,D三点共线。
证: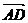 =
= +
+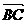 +
+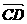 =
=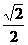 (a+5b) + ( -2a
+ 8b)
+ 3(a
-b)
(a+5b) + ( -2a
+ 8b)
+ 3(a
-b)
= (1+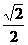 )a + (5 + 5
)a + (5 + 5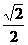 )b = (1+
)b = (1+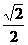 )(a + 5b)
)(a + 5b)
而 =
=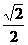 (a+5b)
∴
(a+5b)
∴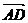 = (
= (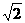 + 1)
+ 1)
又∵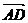 ,
,  有公共点 ∴A,B,D三点共线
有公共点 ∴A,B,D三点共线
2.证明:三角形重心与顶点的距离等于它到对边中点的距离的两倍。
 证:设
证:设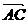 = b,
= b,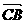 = a,则
= a,则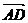 =
=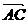 +
+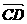 = b+
= b+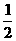 a,
a, 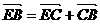 =
=
∵A, G, D共线,B, G, E共线
∴可设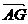 =λ
=λ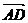 ,
,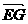 = μ
= μ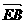 ,
,
则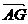 =λ
=λ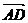 =λ(b+
=λ(b+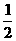 a)=λb+
a)=λb+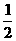 λa,
λa,
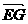 = μ
= μ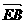 = μ(
= μ(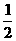 b+a)=
b+a)=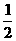 μb+μa,
μb+μa,
∵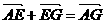 即:
即: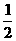 b + (
b + (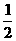 μb+μa) =λb+
μb+μa) =λb+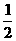 λa
λa
∴(μ-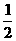 λ)a + (
λ)a + (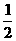 μ-λ+
μ-λ+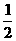 )b = 0 ∵a, b不平行,
)b = 0 ∵a, b不平行,
∴
即:AG = 2GD 同理可化:AG = 2GD , CG = 2GF
1.如图:已知MN是△ABC的中位线,
求证:MN=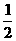 BC, 且MN∥BC
BC, 且MN∥BC
证:∵MN是△ABC的中位线,
∴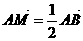 ,
, 
∴
∴MN=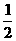 BC, 且MN∥BC
BC, 且MN∥BC
7.在湖面上高h处,测得云彩仰角为a,而湖中云彩影的俯角为b,
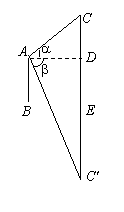 求云彩高。
求云彩高。
解:C、C’关于点B对称,设云高CE = x,
则CD = x - h,C’D = x + h,
 在Rt△ACD中,
在Rt△ACD中,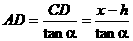
在Rt△AC’D中,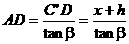
∴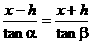 解得:
解得: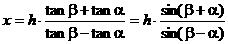
6.某船在海上航行中不幸遇险,并发出呼救信号,我海上救生艇在A处获悉后,立即测出该船的方位角为45°,与之相距10 nmail的C处,还测得该船正沿方位角105°的方向以每小时9 nmail的速度向一小岛靠近,我海上救生艇立即以每小时21 nmail的速度前往营救,试求出该海上救生艇的航向及与呼救船相遇所需时间。
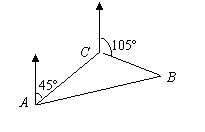 解:设所需时间为t小时,
解:设所需时间为t小时,
在点B处相遇(如图)
在△ABC中,ÐACB = 120°,
AC = 100, AB = 21t, BC = 9t
由余弦定理:(21t)2 = 102 + (9t)2 - 2×10×9t×cos120°
整理得:36t2 -9t - 10 = 0 解得: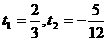 (舍去)
(舍去)
由正弦定理: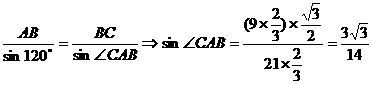
∴ÐCAB = 21°47’
5.一块直径为30cm的圆形铁板,已经截去直径分
别为20cm,10cm的圆形铁板各一块,现要求
在所剩余的铁板中,再截出同样大小的铁板两块,
问:这两块铁板的半径最大有多少cm?
解:设所求最大圆的半径为x,
则在△ABC中:
又在△ACD中: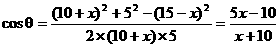
∴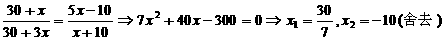
4.如图:在斜度一定的山坡上的一点A测得
山顶上一建筑物顶端C对于山坡的斜度为
15°,向山顶前进100m后,又从点B测得
斜度为45°,假设建筑物高50m,
求此山对于地平面的斜度q。
解:在△ABC中,AB = 100m , ÐCAB = 15°, ÐACB = 45°-15° = 30°
由正弦定理: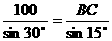 ∴BC = 200sin15°
∴BC = 200sin15°
在△DBC中,CD = 50m , ÐCBD = 45°, ÐCDB = 90° + q
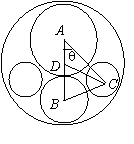 由正弦定理:
由正弦定理: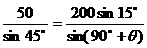 Þcosq =
Þcosq =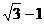 ∴q = 42.94°
∴q = 42.94°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com