3.关于函数图象的变化，正确的结论是 ( 　　) A、将图象y=sin(2x-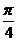)向右平移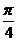，得图象y=sin2x B、将图象y=sin(2x-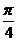)上的每一点的纵坐标不变，横坐标变为原来的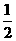，得　　　　　　　 　图象y=sin(x-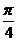) C、将图象y=f(x)按向量=(h,k)平移得图象y=f(x-h)-k D、将图象y=f(x)先按向量平移，再按向量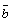平移，且+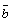=(-1,2)，则得到的图象为y=f(x+1)+2

2.如果f(x+π)=f(-x),且f(x)= f(-x),则f(x)可能是(　　 )

　A、sin2x　　　 Bcosx　　　　　 C、sin|x|　　　 D、|sinx|

1.给出下列关系式：sin1>sin2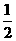,cos(-)>cos,tan125°>tan70°,

sin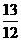π>cos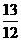π,其中正确的个数是 ( 　　) A、1　　　　　 B、2　　　　　 C、3　　　　　 D、4

高中数学从学习方法和思想方法上更接近于高等数学。学好它，需要我们从方法论的高度来掌握它。我们在研究数学问题时要经常运用唯物辩证的思想去解决数学问题。数学思想，实质上就是唯物辩证法在数学中的运用的反映。中学数学学习要重点掌握的的数学思想有以上几个：集合与对应思想，初步公理化思想，数形结合思想，运动思想，转化思想，变换思想。

例如，数列、一次函数、解析几何中的直线几个概念都可以用函数(特殊的对应)的概念来统一。又比如，数、方程、不等式、数列几个概念也都可以统一到函数概念。

再看看下面这个运用“矛盾”的观点来解题的例子。

已知动点Q在圆x²+y²=1上移动，定点P(2，0)，求线段PQ中点的轨迹。

分析此题，图中P、Q、M三点是互相制约的，而Q点的运动将带动M点的运动；主要矛盾是点Q的运动，而点Q的运动轨迹遵循方程x₀²+y₀²=1①；次要矛盾关系：M是线段PQ的中点，可以用中点公式将M的坐标(x，y)用点Q的坐标表示出来。</P< p>

4、　 要求提高

3、　 难度增大

2、　 课程增多

往往有同学进入高中以后不能适应数学学习，进而影响到学习的积极性，甚至成绩一落千丈。为什么会这样呢？让我们先看看高中数学和初中数学有些什么样的转变吧。

1、　 理论加强

(一)　 数学的三大特点 严谨性、抽象性、广泛的应用性

所谓数学的严谨性，指数学具有很强的逻辑性和较高的精通性，一般以公理化体系来体现。

什么是公理化体系呢？指得是选用少数几个不加定义的概念和不加逻辑证明的命题为基础，推出一些定理，使之成为数学体系，在这方面，古希腊数学家欧几里得是个典范，他所著的《几何原本》就是在几个公理的基础上研究了平面几何中的大多数问题。在这里，哪怕是最基本的常用的原始概念都不能直观描述，而要用公理加以确认或证明。

中学数学和数学科学在严谨性上还是有所区别的，如，中学数学中的数集的不断扩充，针对数集的运算律的扩充并没有进行严谨的推证，而是用默认的方式得到，从这一点看来，中学数学在严谨性上还是要差很多，但是，要学好数学却不能放松严谨性的要求，要保证内容的科学性。

比如，等差数列的通项是通过前若干项的递推从而归纳出通项公式，但要予以确认，还需要用数学归纳法进行严格的证明。

数学的抽象性表现在对空间形式和数量关系这一特性的抽象。它在抽象过程中抛开较多的事物的具体的特性，因而具有十分抽象的形式。它表现为高度的概括性，并将具体过程符号化，当然，抽象必须要以具体为基础。

至于数学的广泛的应用性，更是尽人皆知的。只是在以往的教学、学习中，往往过于注重定理、概念的抽象意义，有时却抛却了它的广泛的应用性，如果把抽象的概念、定理比作骨骼，那么数学的广泛应用就好比血肉，缺少哪一个都将影响数学的完整性。高中数学新教材中大量增加数学知识的应用和研究性学习的篇幅，就是为了培养同学们应用数学解决实际问题的能力。

我们来看看一个生活中有趣的问题。

在任何一次集会中，握过奇数次手的人必有偶数个，试证明。

如果抓住两个关键：一是握手总次数必为偶数，

22、已知函数y=cos(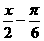)－sin()

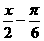(1)求此函数的单调递减区间

(2)写出此函数图象的对称中心及对称轴方程