12.不等式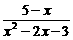≤－1的解集为_______.

本题考查分式不等式的解法.

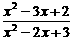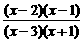[解析] 原不等式等价于≤0

≤0

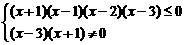
由数轴标根法可知原不等式解集为：

{x|－1＜x≤1或2≤x＜.

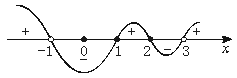
[答案]{x|－1＜x≤1或2≤x＜

11.用描述法表示图中阴影部分的点(包括边界上的点)的坐标的集合应为_______.

本题考查平面内常用点集的表述方法.

[答案] {(x,y)|－1≤x≤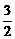,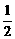－≤y≤1,xy≥0}.

10.若|x－4|+|x－3|＞a对一切实数x恒成立，则实数a的取值范围是(　　 )

A.(－∞,3)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.(－∞,1)　　　

C.[1,+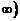　　　 　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－∞,3)∪(4,+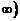

本题考查含两个绝对值符号的不等式的解法.

[解析] [解法一] (1)当x≥4时，|x－4|+|x－3|=(x－4)+(x－3)=2x－7≥1;

(2)当3≤x＜4时，|x－4|+|x－3|=－(x－4)+(x－3)=1;

(3)当x＜3时，|x－4|+|x－3|=－(x－4)－(x－3)=－2x+7＞1.

综上(1)(2)(3)可知，对一切实数x,都有|x－4|+|x－3|≥1.

∴满足条件的a的取值范围为a＜1.

[解法二] 如图

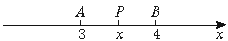
∵|x－4|+|x－3|=|PA|+|PB|≥1

∴满足条件的a的取值范围为a＜1

[解法三] 由|x－4|+|x－3|≥|(x－4)－(x+3)|=1

可知满足条件的a的取值范围为a＜1.

[答案] B

第Ⅱ卷(非选择题　 共70分)

9.设U={1,2,3,4,5},若A∩B={2},(_UA)∩B={4}，(_UA)∩(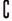_UB)={1，5}，则下列结论正确的是(　　 )

A.3A且3B　　　　　　 B.3B且3∈A　　　　　　 C.3A且3∈B　　　　　　 D.3∈A且3∈B

本题考查集合的运算.

[解析] 解答本题可利用文氏图填空的办法.

如图，∵A∩B={2},(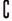_UA)∩B={4},(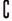_UA)∩(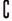_UB)={1,5}.

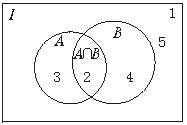
∴3必在A∩(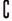_UB)中，∴3∈A,但3B.

[答案] B

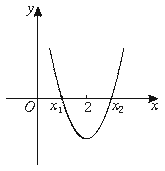
8.二次函数y=x²+(a－3)x+1的图象与x轴的两个交点的横坐标分别为x₁,x₂,且x₁＜2,x₂＞2,则a的取值范围是(　　 )

A.a＜1或a＞5　　　　　　　　　　　　　　　　　　　　　　　　 B.a＜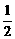

C.a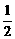＜－或a＞5　　　　　　　　　　　　　　　　　　　　　 D.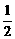－ ＜a＜1

本题考查由一元二次函数的图象求参数范围的问题.

[解析] 依题意可得,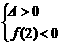

即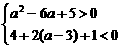

解得a＜.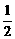

[答案] B

7.已知M={x|x=3k,k∈Z},P={x|x=3k+1,k∈Z},Q={x|x=3k－1,k∈Z},若a∈M,b∈P,c∈Q,则a+b－c∈(　　 )

A.M　　　　　　　　　　　　　　 B.P　　　　　　　　　　　　　　　 C.Q　　　　　　　　　　　　　　 D.M∪P

本题考查元素与集合间关系的判定.

[解析] 设a=3k₁,b=3k₂+1,c=3k₃－1.

则a+b－c=3(k₁+k₂－k₃)+2=3(k₁+k₂－k₃+1)－1,而k₁+k₂－k₃+1∈Z.

[答案] C

6.已知集合A={－1,1},B={x|mx=1},且A∪B=A,则m的值为(　　 )

A.1　　　　　　　　 　　　 　　　 B.－1　　　　　　　　　　　　　 C.1或－1　　　 　　　　　　　 D.1或－1或0

本题考查集合间的关系及分类讨论的能力.

[解析] 由A∪B=A有B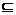A,

①当m=0时，有B=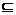A

②当m≠0时，有B={x|x=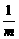}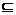A

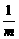∴=1或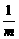=－1,∴m=1或m=－1.

综上可知m=0或m=1或m=－1.

[答案] D

5.若x是不等式组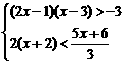的解，则P(x+2, x－2)?在(　　 )

A.第一象限　　　　　　　　　 B.第二象限　　　　　　　　　 C.第三象限　　　　　　　　　 D.第四象限

本题考查一元二次不等式组的解法.

[解析] 由原不等式组得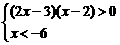，解得x＜－6

∵x+2＜－4,x－2＜－8,

∴点P(x+2,x－2)在第三象限.

[答案] C

4.集合A={x|x²－3x－10≤0,x∈Z},B={x|2x²－x－6＞0, x∈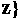,则A∩B的非空真子集的个数为(　　 )

A.16　　　　　　　　　　　　　　　　　 B.14　　　　　　　　　　　　　　　　　 C.15　　　　　　　　　　　　　　　　　 D.32

本题考查一元二次不等式的解法及求交集、子集的有关知识.

[解析] 易得A={x|－2≤x≤5,x∈Z},B={x|x＞2或x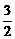＜－,x∈Z＝.

∴A∩B={x|－2≤x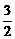＜－或2＜x≤5,x∈Z}={－2,3,4,5}.

下面就是求集合{－2，3，4，5}的非空真子集的个数，我们知道，一个集合若有n个元素，则它的子集共有2ⁿ个，其中真子集有2ⁿ－1个，非空真子集有2ⁿ－2个，因此，本题答案为2⁴－2=14个.

[答案] B

[答案] C

3.已知M={x|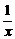＜,N={y|y=x²},则M∩N等于(　　 )

A.　　　　　　　　　　　　　　　　　　 B.{x|x＞1}

C.{x|x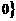＜　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.{x|x＜0或x＞1}

本题考查集合的元素及交集运算.

[解析] M={x|x＞1或x＜0},N={y|y≥0},两个集合都是数集，集合中的元素是数，易知M∩N={x|x＞1}.

[答案] B