
题目列表(包括答案和解析)
2.一条弦长等于半径的  ,则此弦所对圆心角( ).
,则此弦所对圆心角( ).
A.等于  弧度 B.等于
弧度 B.等于  弧度
弧度
C.等于  弧度 D.以上都不对
弧度 D.以上都不对
1.  的值是( ).
的值是( ).
A.  B.
B. 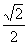 C.
C.  D.
D. 
0.1x+0.01x2>12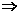 x2+10x-1200>0
x2+10x-1200>0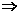 x>30或x<-40(舍去)
x>30或x<-40(舍去)
根据题意,甲车刹车距离略超过12米
∴甲车速不会超过30千米/时很多;
对于乙车:0.05x+0.005x2>10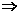 x2+10x-2000>0
x2+10x-2000>0
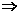 x>40或x<-50(舍去)
x>40或x<-50(舍去)
∵乙车速已经大于弯道限速40千米/时,
∴主要责任在乙.
19.(本小题满分12分)
汽车在行驶中,由于惯性作用,刹车后还要继续向前滑引一段距离才能停住,我们将这段距离称为“刹车距离”.刹车距离是分析事故的一个重要因素,在一个限速为40千米/时以内的弯道上,甲乙两辆车相向而行,发现情况不对,同时刹车,但还是相碰了,事后现场测得甲车的刹车距离超过了12米,乙车的刹车距离超过了10米,已知甲乙两种车型的刹车距离S(米)与车速x(千米/时)之间有如下关系:
S甲=0.1x+0.01x2,S乙=0.05x+0.005x2
问两车相碰的主要责任是谁?
本题考查学生解应用题及不等式的能力.
[解] 由题意知,对于甲车:
18.(本小题满分12分)
已知集合A={x|-x2+x+2<0},B={x|2x2+(2k+5)x+5k<0,k∈R}.求A∩B;
本题考查含参数不等式的解法及利用数轴求集合的子集.
[解] A={x|x>2或x<- ,B={x|(x+
,B={x|(x+ )(x+k)<
)(x+k)<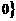 .
.
①当k> 时,B={x|-k<x<-
时,B={x|-k<x<- .
.
由图(1)可知A∩B={x|-k<x<- .
.

图(1)
②当k= 时,B=
时,B= ,A∩B=
,A∩B= .
.
③当k< 时,B={x|-
时,B={x|- <x<-
<x<- .
.
(i)当- <-k≤-1即1≤k<
<-k≤-1即1≤k< 时,
时,
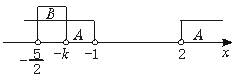
图(2)
由图(2)可知A∩B={x|- <x<-k}
<x<-k}
(ii)当-1<-k≤2即-2≤k<1时,
由图(3)知A∩B={x|- <x<-
<x<- .
.

图(3)
(iii)当-k>2即k<-2时,
由图(4)可知A∩B={x|- <x<-1或2<x<-
<x<-1或2<x<- .
.

图(4)
17.(本小题满分12分)
已知集合A={x|x2-4x+3<0},B={x||x-3|≤1}.
(1)试定义一种新的集合运算Δ,使AΔB={x|1<x<2};
(2)按(1)的运算,求出BΔA.
本题考查学生对集合交、并、补集定义的理解及相关知识的联系与迁移能力,培养学生的发散性思维和创造性思维.
[解] 易得A={x|1<x<3},B={x|2≤x≤4}.
(1)∵AΔB={x|1<x< ,
,

由图可知AΔB中的元素都在A中但不在B中,
∴定义AΔB={x|x∈A且x B}.
B}.
(2)由(1)可知BΔA={x|x∈B且x A}={x|3≤x≤4}.
A}={x|3≤x≤4}.
16.(本小题满分10分)
已知集合A={x|-2<x<-1或x>1},B={x|x2+ax+b≤0},且A∩B={x|1<x≤3},A∪B={x|x≥-2},试求a,b的值.
本题考查集合间的运算.
这样的定集合与动集合之间的运算通常是利用数轴进行子、交、并、补的运算,也就是简单的数形结合问题.
[解] 如图,可知B={x|-1≤x≤3}.

即-1≤x≤3是不等式x2+ax+b≤0的解集.
∴ ,解得
,解得 .
.
15.(本小题满分8分)
已知集合A={x|x2-5x+6<0},B={x|x2-4ax+3a2<0}且A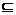 B,求实数a的取值范围.
B,求实数a的取值范围.
本题考查含参数的一元二次不等式的解法,集合的交、并运算及分类讨论的能力.
[解] A={x|x2-5x+6<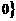 ={x|2<x<
={x|2<x< ,
,
B={x|x2-4ax+3a2<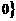 ={x|(x-a)(x-3a)<
={x|(x-a)(x-3a)<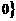
(1)当a>0时,B={x|a<x<3a},
∵A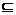 B,∴
B,∴ ,解得1≤a≤2.
,解得1≤a≤2.
(2)当a<0时,B={x|3a<x<a}.
由A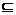 B,得
B,得 ,解集为
,解集为 .
.
(3)当a=0时,B={x|x2<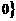 =
= 不合题意.
不合题意.
综上(1)(2)(3)可知1≤a≤2.
14.已知关于x的不等式|x- |≤
|≤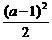 的解集是单元素集A,则a=____,A=_____.
的解集是单元素集A,则a=____,A=_____.
本题考查含绝对值不等式的解法.
[解析] 由|x- |≤
|≤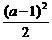 解得2a≤x≤a2+1
解得2a≤x≤a2+1
又∵不等式的解集为单元素集,∴a2+1=2a,
解得a=1,此时A={2}.
[答案] 1 {2}
13.已知集合P={x|x2+(m+2)x+1=0,x∈R},若P∩{正实数}= ,则实数m的取值范围为_______.
,则实数m的取值范围为_______.
本题考查集合与方程及分类讨论思想,注意在有关子集讨论中不要忽视对空集的讨论.
[解析] (1)当P= 时,有Δ=(m+2)2-4<0,解得-4<m<0.
时,有Δ=(m+2)2-4<0,解得-4<m<0.
(2)当P≠ 时,有
时,有
解得 ,得m≥0
,得m≥0
综上①②可知m>-4.
[答案] {m|m>-4}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com