41．某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P最多2500件，月产Q最多1200件.而组装一件P需4个A，2个B；组装一件Q需6个A，8个B.某个月该厂能用的A最多有14000个，B最多有12000个.已知产品P每件利润1000元，Q每件利润2000元，欲使该月利润最高，需组装P、Q产品各多少件?最高利润多少万元?

40．开始时，烧瓶里有N个细菌，每小时末，细菌的数量和这一小时初的细菌数量相比增加10%，除此以外，在每小时末，从烧瓶里取出含有n个细菌的一份，问经过n小时后，烧瓶里的细菌的数量(取出相应的份数后)就超过开始时细菌数量的一倍?并确定有解的条件．

39、我国是水资源比较贫乏的国家之一，各地采用价格调控手段来达到节约用水的目的.某市用水收费的方法是：水费＝基本费+超额费+损耗费.若每月用水量不超过最低限量a m³时，只付基本费8元和每户每月定额损耗费c元，若用水量超过a m³时，除了付同上的基本费和损耗费外，超过部分每m³付b元的超额费.已知每户每月的定额损耗费不超过5元.

该市一家庭今年第一季度的用水量和支付费用如表所示：

试根据上面表格中的数据求a、b、c.

38. 有甲、乙两个粮食经销商，每次同时、同地、同价格购进粮食(随市场调节，每次粮价可能不同)，它们各购粮3次，甲每次购粮10000kg，乙每次购粮用10000元，规定谁平均每千克支付的粮款少，谁的购粮方式就更经济，试判断甲、乙两人谁的购粮方式更经济？并证明你的结论。

37. 某公司生产一种产品，每年需投入固定成本0.5万元，此外每生产100件这种产品还需投资2.5万元，经预测知市场对这种产品的年需求量为500件，且当售出这种产品的数量为t(单位：百件)时，销售所得收入约为5t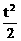－万元，(I)若该公司这种产品的年产量为x(单位：百件, x>0)，试把该公司生产销售这种产品的年利润表示为当年产量x的函数；

(II)当该公司的年产量多大时，当年所得利润最大，

(III)当该公司的年产量多大时，当年不会亏本？

36. 甲、乙两地相距40公里，某人以每小时V公里的速度骑车由甲赴乙，到达乙后，他以原速度返回，行至某处，因故停留了20分钟，停留后他以比原速度每小时快4公里的速度继续前进，若他由乙地返回甲地的的归途中所用的时间不比从甲地到乙地所用的时间多，求V的取值范围。

35. 某企业经过调整后，第一年资金增长率为300%，以后每年的增长率都是前一年增长率的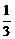，(I)经过4年后，企业资金是原资金的多少倍？(II)若由于某种原因每年损失资金的5%，那么经过多少年后，企业的资金开始下降？

34. 某企业在“减员增效”中，对部分人员实行分流，规定分流人员第一年可以到原单位领取工资的100%，从第二年起，以后每年只能在原单位按上一年的领取工资。该企业根据分流人员的技术特长，计划创办新的经济实体，该实体预计，第一年属投资阶段没有利润，第二年每人可获得b元收入，从第三年起，每人收入可在上一年的基础上递增50%。如果某人分流前每年收入为a元，分流后第n年收入为a _n元，(I)求a _n；(II)当b=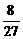a时,这个人哪一年收入最少？最少是多少元？(III)当b≥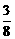a时，是否可以保证这个人分流一年后的年收入永远超过分流前的年收入？

33. 某河流一段区域，汛前的水位为120cm，水位警戒线高为300cm，水位超过警戒线时，河坝就会发生危险，预测汛期来临时，水位线的提高量L_n与汛期天数n的函数关系为L_n=20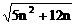，为防止河坝发生危险，堤坝上有泄水涵道，每天泄水量可使水位线下降40cm，如果从汛期来临的第一天起，就开始泄水排洪，试问从第几天起河坝会出现险情？

32. 生产某种商品x吨，所需费用为(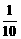x²+5x+1000)元，而售出x吨这种商品时，每吨售价为p元，这里p依关系式p=a+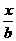(a, b为常数)而定，(I)写出这种商品所获得的利润y元与售出这种商品的吨数x的函数关系式；(II)如果生产出来的这种商品都能卖完，那么当产量是150吨时所获利润最大，并且这时每吨的售价为40元，求a, b的值。