2．对于平面上两个不共线向量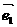，是不是平面上的所有向量都可以用它们来表示？

--提出课题：平面向量基本定理

1．是不是每一个向量都可以分解成两个不共线向量？且分解是唯一？

　　　　　　 P124　 习题5.8

3．按题设，这种平移是使点O’ (-2, 3)移到O(0, 0)，

设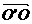= (m, n)　 则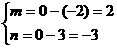

设P(x, y)是抛物线y = x² + 4x + 7上任一点，对应点P’为(x’, y’)

则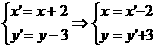　 代入y = x² + 4x + 7得：y’ = x’²　

即：y = x²

2．求将这条抛物线平移到顶点与原点重合时的函数解析式。

　　　　 解：1．设抛物线y = x² + 4x + 7的顶点O’坐标为(h, k)

　　　　　　　 则h = -2,　 k = 3　　 ∴顶点O’坐标为(-2, 3)

1．求抛物线顶点坐标。

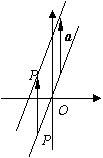　 解：设P(x, y)为l上任一点，它在l’上的对应点为P’(x’, y’)

　　　 由平移公式：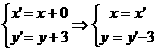

　　　 代入y = 2x得：y’ - 3 = 2x’　 　即：y’ = 2x’ + 3

　　　 按习惯，将x’、y’写成x、y得l’的解析式：y = 2x + 3

　　　 (实际上是图象向上平移了3个单位)

2．由平移公式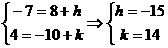：即a的坐标为(-15, 14)

2．点M(8, -10)按a平移后对应点M’的坐标为(-7, 4)，求a。

　　　 解：1．由平移公式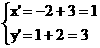：　 即对应点A’的坐标为(1, 3)

1．把点A(-2, 1)按a = (3, 2)平移，求对应点A’的坐标(x’, y’)。