
题目列表(包括答案和解析)
1.平面向量数量积的定义、运算、运算律
7.已知点M(2,3),N(8,4),点P在线段MN上,且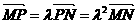 ,
,
求点P坐标和λ。
解:设点P坐标为(x, y),由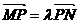 ,
, ,
,
又∵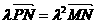 可知λ¹ 0,且
可知λ¹ 0,且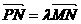 ,
,
从而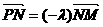 , ∴
, ∴
∴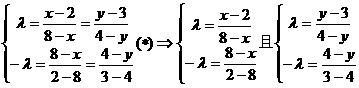
∴

代入检验(*):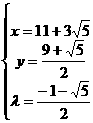 或
或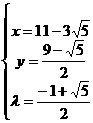
∴点P坐标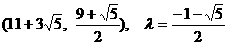
或点P坐标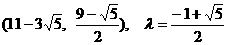
6.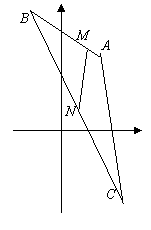 已知A(1,2),B(-1,3),C(2,-2),点M分
已知A(1,2),B(-1,3),C(2,-2),点M分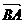 的比λ为3:1,点N在线段BC上,且
的比λ为3:1,点N在线段BC上,且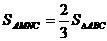 ,求点N的坐标。
,求点N的坐标。
解:由题设: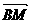 =3
=3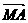 ∴
∴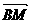 =
=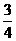
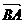
又: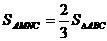 ∴
∴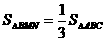
即: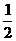 |
|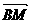 ||
||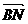 |sinÐABC =
|sinÐABC =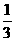 •
•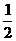 |
|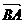 ||
||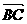 |sinÐABC
|sinÐABC
又 |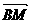 | =
| =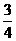 |
|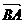 | ∴ |
| ∴ |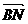 | =
| = 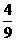 |
|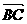 |
|
∴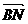 =
=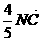 即N分
即N分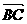 的比为4:5, 设N(x, y)
的比为4:5, 设N(x, y)
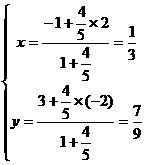 ∴点N的坐标是
∴点N的坐标是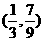
5.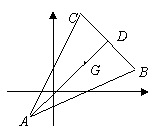 已知△ABC的顶点是A(x1, y1),B(x2, y2),C(x3, y3),求△ABC的重心G的坐标(x, y)。
已知△ABC的顶点是A(x1, y1),B(x2, y2),C(x3, y3),求△ABC的重心G的坐标(x, y)。
解:如图:∵D是BC中点,
∴D点的坐标(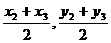 )
)
且G分有向线段AD所成的比λ=2
∴G的坐标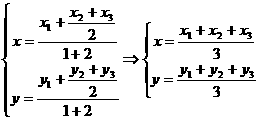
∴△ABC的重心G的坐标是(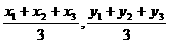 )
)
4.已知M(1,-3),N(4,6),P(x,3),且三点共线,求点P分有向线段MN所成的比λ及x的值。
解: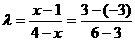
解得:λ= 2, x = 3
3.已知:A(1,-2),B(2,1),C(3,2),D(-2,3),
1°求证:A,B,C三点不共线
2°以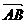 、
、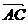 为一组基底来表示
为一组基底来表示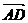 +
+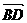 +
+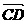
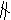 解:1°∵
解:1°∵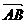 =(1,3),
=(1,3), 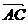 =(2,4) ∵1×4-3×2¹0 ∴
=(2,4) ∵1×4-3×2¹0 ∴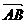
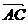
∴A,B,C三点不共线
2°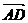 +
+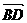 +
+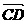 =(-3,5)+(-4,2)+(-5,1) = (-12,8)
=(-3,5)+(-4,2)+(-5,1) = (-12,8)
设: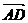 +
+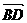 +
+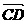 = m
= m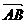 + n
+ n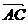
即:(-12,8) = (m + 2n, 3m + 4n)
∴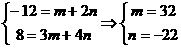 ∴
∴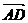 +
+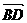 +
+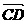 = 32
= 32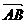 -22
-22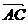
2.设a = (1,x),b = (-1,3),且2a + b∥a -2b,试求x。
解:2a + b = (1,), a -2b = (3, x-6)
∵2a + b∥a -2b ∴1×(x-6) - (2x+3)×3 = 0 Þ x = -3
1.已知四边形的顶点坐标为A(1,2),B(2,5),C(8,14),D(3,5),
求证:四边形ABCD是一个梯形。
证:∵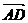 =(2,3),
=(2,3), 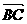 =(6,9) 且2×9-3×6=0 ∴
=(6,9) 且2×9-3×6=0 ∴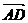 ∥
∥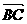
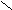 又∵
又∵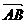 =(1,3),
=(1,3), 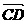 =(-5,-9) 而1×(-9)-3×(-5)¹0 ∴
=(-5,-9) 而1×(-9)-3×(-5)¹0 ∴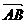 ∥
∥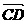
∴ABCD为梯形
解:∵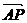 =t
=t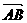
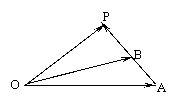 ∴
∴ =
=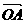 +
+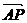 =
=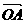 + t
+ t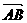
=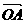 + t(
+ t(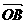 -
-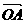 )
)
=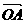 + t
+ t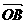 -t
-t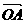
=(1-t) 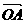 + t
+ t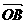
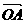 =
=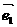
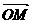 =λ1
=λ1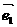
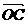 =
= =
=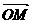 +
+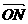 =λ1
=λ1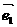 +λ2
+λ2
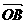 =
=
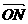 =λ2
=λ2
得平面向量基本定理:如果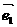 ,
, 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数λ1,λ2使
,有且只有一对实数λ1,λ2使 =λ1
=λ1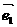 +λ2
+λ2
注意几个问题:1° 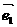 、
、 必须不共线,且它是这一平面内所有向量的一组基底
必须不共线,且它是这一平面内所有向量的一组基底
2° 这个定理也叫共面向量定理
3°λ1,λ2是被 ,
,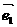 ,
, 唯一确定的数量
唯一确定的数量
2.例一( P106例三)已知向量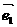 ,
, 求作向量-2.5
求作向量-2.5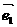 +3
+3 。
。
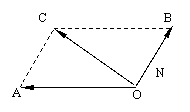
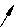
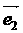
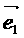 作法:1° 取点O,作
作法:1° 取点O,作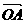 =-2.5
=-2.5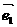
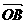 =3
=3

 2° 作 OACB,
2° 作 OACB,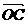 即为所求+
即为所求+
 例二、(P106例4)如图 ABCD的两条对角线交于点M,且
例二、(P106例4)如图 ABCD的两条对角线交于点M,且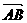 =
= ,
,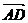 =
=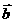 ,
,
用 ,
,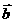 表示
表示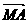 ,
,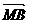 ,
,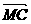 和
和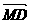
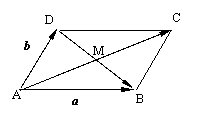
 解:在 ABCD中
解:在 ABCD中
∵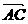 =
=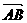 +
+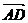 =
= +
+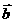
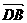 =
=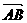 -
-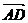 =
= -
-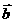
∴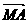 =-
=-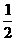
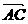 =-
=-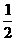 (
( +
+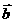 )=-
)=-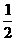
 -
-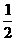
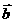
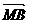 =
=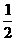
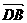 =
=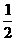 (
( -
-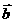 )=
)=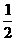
 -
-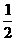
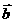
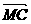 =
=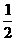
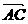 =
=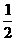
 +
+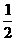
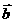
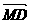 =-
=-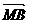 =-
=-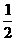
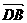 =-
=-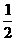
 +
+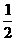
 例三、已知 ABCD的两条对角线AC与BD交于E,O是任意一点,
例三、已知 ABCD的两条对角线AC与BD交于E,O是任意一点,
求证: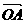 +
+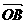 +
+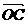 +
+ =4
=4
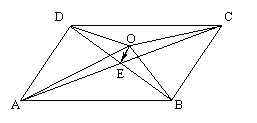 证:∵E是对角线AC和BD的交点
证:∵E是对角线AC和BD的交点
∴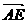 =
=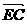 =-
=-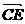
 =
=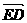 =-
=-
在△OAE中 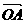 +
+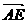 =
=
同理: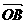 +
+ =
=
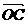 +
+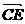 =
=
 +
+ =
=
以上各式相加,得: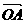 +
+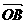 +
+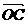 +
+ =4
=4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com