解：设x = (t, s)，

　　　　　 由x×a = 9 Þ 3t - s = 9　　　 s = -3

　　　　　 ∴x = (2, -3)

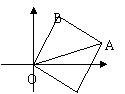例四、如图，以原点和A(5, 2)为顶点作等腰直角△OAB，使ÐB = 90°，

　　　 求点B和向量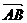的坐标。

　　　 解：设B点坐标(x, y)，则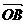= (x, y)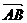，= (x-5, y-2)

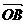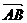　　　　　 ∵^　 ∴x(x-5) + y(y-2) = 0即：x² + y² -5x - 2y = 0

　　　　 又∵|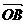| = ||　 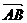∴x² + y² = (x-5)² + (y-2)²即：10x + 4y = 29

　　　　 由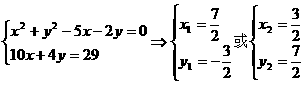

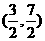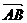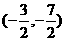　　　　 ∴B点坐标或；=或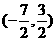

4．例二、已知A(1, 2)，B(2, 3)，C(-2, 5)，求证：△ABC是直角三角形。

　　 　证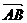：∵=(2-1, 3-2) = (1, 1),　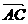 = (-2-1, 5-2) = (-3, 3)

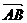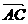　　　　 ∴×=1×(-3) + 1×3 = 0　 ∴^

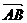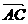
　　　　 ∴△ABC是直角三角形

　 解：a×b = 5×(-6) + (-7)×(-4) = -30 + 28 = -2

3．长度、角度、垂直的坐标表示

　 1°a = (x, y)　 Þ　 |a|² = x² + y² Þ　 |a| =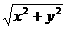

　　　　 2°若A = (x₁, y₁)，B = (x₂, y₂)，则=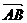

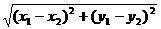
　　　　 3° cosq =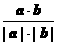

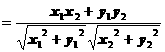
　　　　 4°∵a^b Û a×b = 0 即x₁x₂ + y₁y₂ = 0(注意与向量共线的坐标表示原则)

2．推导坐标公式：

　 ∵a = x₁i + y₁j,　 b = x₂i + y₂j

　 ∴a×b = (x₁i + y₁j )(x₂i + y₂j) = x₁x₂i² + x₁y₁i×j + x₂y₁i×j + y₁y₂j²

　　　　 = x₁x₂ + y₁y₂

从而获得公式：a×b = x₁x₂ + y₁y₂

1．设a = (x₁, y₁)，b = (x₂, y₂)，x轴上单位向量i，y轴上单位向量j，

　 则：i×i = 1，j×j = 1，i×j = j×i = 0

4．两向量共线的坐标表示：

3．两平面向量垂直的充要条件

2．平面向量数量积的运算

1．平面向量的坐标表示及加、减、实数与向量的乘积的坐标表示

　　　　 　　　　　习题5.6　　 1-6