
题目列表(包括答案和解析)
a - 4b与7a - 2b垂直,求a与b的夹角。
解:由(a + 3b)(7a - 5b) = 0 Þ 7a2 + 16a×b -15b2 = 0 ①
(a - 4b)(7a - 2b) = 0 Þ 7a2 - 30a×b + 8b2 = 0 ②
两式相减:2a×b = b2
代入①或②得:a2 = b2
设a、b的夹角为q,则cosq = ∴q = 60°
∴q = 60°
4.例题:P118-119 例二、例三、例四 (从略)
3.(a + b)×c = a×c + b×c
 在平面内取一点O,作
在平面内取一点O,作 = a,
= a,  = b,
= b, = c,
= c,
∵a + b (即 )在c方向上的投影
)在c方向上的投影
等于a、b在c方向上的投影和,
即:|a + b| cosq = |a| cosq1 + |b| cosq2
∴| c | |a + b| cosq =|c| |a| cosq1 + |c| |b| cosq2
∴c×(a + b) = c×a + c×b 即:(a + b)×c = a×c + b×c
2.( a)×b =
a)×b = (a×b) = a×(
(a×b) = a×( b)
b)
证:若 > 0,(
> 0,( a)×b =
a)×b = |a||b|cosq,
|a||b|cosq,
 (a×b) =
(a×b) = |a||b|cosq,
|a||b|cosq,
a×( b) =
b) = |a||b|cosq,
|a||b|cosq,
若 < 0,(
< 0,( a)×b =|
a)×b =| a||b|cos(p-q) = -
a||b|cos(p-q) = - |a||b|(-cosq) =
|a||b|(-cosq) = |a||b|cosq,
|a||b|cosq,
 (a×b) =
(a×b) = |a||b|cosq,
|a||b|cosq,
a×( b) =|a||
b) =|a|| b|cos(p-q) = -
b|cos(p-q) = - |a||b|(-cosq) =
|a||b|(-cosq) = |a||b|cosq。
|a||b|cosq。
1.交换律:a × b = b × a
证:设a,b夹角为q,则a × b = |a||b|cosq,b × a = |b||a|cosq
∴a × b = b × a
2.判断下列各题正确与否:
1°若a = 0,则对任一向量b,有a×b = 0。 ( √ )
2°若a ¹ 0,则对任一非零向量b,有a×b ¹ 0。 ( × )
3°若a ¹ 0,a×b = 0,则b = 0。 ( × )
4°若a×b = 0,则a 、b至少有一个为零。 ( × )
5°若a ¹ 0,a×b = a×c,则b = c。 ( × )
6°若a×b = a×c,则b = c当且仅当a ¹ 0时成立。 ( × )
7°对任意向量a、b、c,有(a×b)×c ¹ a×(b×c)。 ( × )
8°对任意向量a,有a2 = |a|2。 ( √ )
1.平面向量数量积(内积)的定义及其几何意义、性质
《教学与测试》P154 5、6、7、8,思考题
长度、夹角、垂直的坐标表示
求k值。
解:当A = 90°时,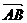 ×
×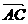 = 0,∴2×1 +3×k = 0 ∴k =
= 0,∴2×1 +3×k = 0 ∴k =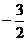
当B = 90°时,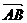 ×
× = 0,
= 0, =
=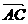 -
-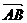 = (1-2, k-3)
= (-1, k-3)
= (1-2, k-3)
= (-1, k-3)
∴2×(-1) +3×(k-3) = 0 ∴k =
当C = 90°时,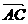 ×
× = 0,∴-1 + k(k-3) = 0 ∴k =
= 0,∴-1 + k(k-3) = 0 ∴k =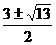
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com